Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros
-
JulkaisijaArtikkelit
-
kannattaa jatkaa mailanpään vauhdin kasvattamista, se on se suurin avain pallon lähtönopeuden petraamiseen
Edellyttäen, että onnistut säilyttämään muut osuman ”hyvyyteen” vaikuttavat tekijät 😎… oman kokemuksen mukaan useimmiten ”90% teholla” lyöminen tuottaa suurimman pallon lähtönopeuden.
Eli aivan täysiä draivatessa smash factor on usein jossain 1,35 tasolla, kun hieman rauhallisemmassa lyönnissä sen saa 1,45..1,47 tasolle. Jos ajatellaan, että täysiä draivatessa saat mailanpään nopeutta 115 mph, niin pallo lähtee 155 mph. Rauhallisemmassa swingissä lyöt 110 mph ja pallo lähtee yli 159 mph.
PG
Swinger?
Esim, kun se varsi on kerran taipuvaa sorttia, niin enkö muka pysty lyömään niin että palloa lähestyessä ja palloon tullessa varsi on vielä taipuneena ja siinä on siis jousivoimaa viritettynä? Ja, joka purkautuu osuman aikana (voi osittain alkaa jo vähän ennen sitä, tai sitten ei, mun mielestä ole oleellisesta merkitystä kunhan jousivoimaa on vielä osumaan tullessa jäljellä). Ja, tuloksena on (mun mielestä) se, että pallo puristuu vähän enemmän kasaan kuin ilman ko jousivoiman vaikutusta – ja pallo saa suuremman lähtönopeuden.Jos osumaan tullessa varsi on taaksepäin taipuneena ts. jousivoimaa on vielä jäljellä, niin vastaava varastossa oleva jousienergia pallon lähtönopeuden lisäämiseksi jää kontaktiajan lyhyyden takia lähes kokonaan hyödyntämättä. Jousivoima kannattaa käyttää mailanpään nopeuden lisäämiseen.
Jäin miettimään tätä. PG:n logiikka on vahva, joten epäröin kyllä itsekin. Siitä huolimatta tuumin seuraavaa.
Se että mailojen COR arvoille on määritelty maksimi perustuu, jos oikein luin ja ymmärsin, siihen että jos mailan (metalli)pinta joustaa, niin se aiheuttaa jousivoiman osumassa. Tuo jousto puolestaan vähentää pallon puristumista (vähentää pallon puristumisen energiahäviötä), mikä puolestaan lisää pallon lähtönopeutta. Joten, tuolle määriteltiin raja paljonko lavan pinta saa joustaa.
Tuosta tuli mieleen myös aiemmin viitattu testi, jossa driverin mailanpään nopeuden kasvaessa osumahetken kesto lyhenee ja arvio siitä että pallosta tulee jäykempi kun osuman vauhti (ja siten osuman voiman vaikutus) kasvaa.
Noita kahta asiaa vasten, tuo mun ylläreferoitu ajatus on ilmeisesti taas ajatusharha – jos mailan varrella olisi jännitettyä jousivoimaa osumaan tullessa, niin se ei itse asiassa puristaisi palloa enempää kasaan, vaan luultavasti kävisikin päinvastoin. Pallo puristuu vähemmän kasaan mutta pallo saa isomman lähtönopeuden sen takia.
Sitten varsinainen kysymys. Kannattaako antaa (rauta)mailan varren jännityksen purkautua niin että se lisää lavan vauhtia (mikä lisää pallon lähtönopeutta); vai ylläpitää ko jännitystä osumaan asti ja siten lyödä palloa ’kovempaa’ (vauhti + lisäjousivoima), jolloin pallo saisi myös isomman lähtönopeuden. Tuossa olisi silloin kaksi jousta vastakkain, eli onko kysymys toisin sanoen se, että kumpi jousi on jäykempi?
Impaktin aika on tunnetun lyhyt, mutta ilmeisesti tällä asialla on vaikutus koska noita mailojen materiaalien testejäkin tehdään samaan jousivoimaan ja ko impaktin kestoon perustuen.
Täällä on myös paljon perusteltu ’vain vauhti ratkaisee’ faktaa täysvauhtisten driverilyöntien testien perusteella. Ja, osin noiden testien ja niihin perustuvien tutkimusten perusteella, sekä osin liikemäärälaskelmien perusteella, että sama fakta pätee myös rautamailalla lyömiseen. Oma kokemus on tässä asiassa erilainen ja perustelutkin vielä puuttuu, mutta siitä huolimatta mulla on joku marmatusmoodi vielä päällä ja kysymys, että onko välttämättä näin? Rautalyöntien COR arvot ja smash factor on eri tasolla kuin drivereilla, joten niistä pelivaraa on periaatteessa enemmän. Samaten, spinni kasvaa joten energiaa siirtyy myös siihen enemmän, joten driveritutkimukset ei välttämättä kerro kaikkea rautalyönneistä.
Ilmeisesti olen esittänyt asiani kovin epäselvästi, koska tuo ei vastaa ihan sitä, mitä itse olen yrittänyt sanoa:
-Kontaktiaika on alle sadasosa silmänräpäykseen kuluvasta ajasta. Siitä syystä, jos tarkastelu kohdistuu pelaajan osuma-aikaiseen tekemiseen, niin siinä pätee: pelaajan vaikutus on käytännössä merkityksetön, olkoon mailana mikä hyvänsä.
-Draiverilyönteihin voidaan soveltaa yksinkertaisempaa kaava, kuin muille mailoille syyllistymättä kovin suureen vääryyteen. Draiverin mclub = 200 g ja suurin COR = 0,83. Näillä arvoilla ’peruskaava’ swetariosumalla ja optimaalisella osumageometrialla on yksinkertaisesti vball = 1,49*mclub. Draiverilla lyötäessä pallo voi siis saada jopa puolitoistakertaisen vauhdin mailanpään vauhtiin verrattuna.
Tarkemmassa kaavassa (vball = vclub*[(1+COR)*cos(ß)] / [cos(ß – ø) + (1+mball/mclub)*cos(ß)*cos(ø)]) on lisämuuttujina lavan loft, lähtökulma ilmaan ja AoA. Niitä ei voi jättää huomioonottamatta – ei ainakaan rautamailoja käytettäessä. Pelivaraa on paljon. Antamalla kaavan oikealla puolella oleville muuttujille erilaisia arvoja todetaan pallon lähtönopeuden saavan ’jos jonkinlaisia’ arvoja. Tietenkin myös pallon lentorata on jokaiselle tapaukselle ihan omanlaisensa ja täysin erilainen kuin draiverilyönnissä. Esim. PGA tourilla draiveri vs. rautaysi: lähtökulma 11 vs. 20 astetta, maahan iskeytymiskulma 38 vs. 51 astetta. Sen sijaan lakikorkeudessa ei ole paljon eroa. (Mahtuu kaikilla mailoilla 27 m ja 32 m sisään). Oleellinen ero myös draiverin ja r9:n smash factoreissa : 1,48 vs. 1,28.
Itseäni ei suuresti kiinnosta se, miten lyhyellä rautamailalla voisin lyödä mahdollisimman pitkälle. Tosin em. kaavaa soveltamalla siitä saisi kohtuullisen hyvän käsityksen. Spinnin tuottaminen on ihan oma juttunsa, jossa harvoin pituutta tavoittelen.
Sitten varsinainen kysymys. Kannattaako antaa (rauta)mailan varren jännityksen purkautua niin että se lisää lavan vauhtia (mikä lisää pallon lähtönopeutta); vai ylläpitää ko jännitystä osumaan asti ja siten lyödä palloa ’kovempaa’ (vauhti + lisäjousivoima), jolloin pallo saisi myös isomman lähtönopeuden. Tuossa olisi silloin kaksi jousta vastakkain, eli onko kysymys toisin sanoen se, että kumpi jousi on jäykempi?
Kannattaa, sillä jos vasta osumassa varren jännitystä yritetään hyödyntää, aikaa on käytettävissä vain sadasosa silmänräpäystä. Aivan liian vähän.
Jännityksen ylläpitäminen edellyttää mailanpään kiihdyttämistä. Jos kiihtyvyys juuri ennen osumaa on esim. 100 m/s^2 (ja varsi taaksepäin taipunut), niin kyse on samasta asiasta, jota olen jo aiemmin käsitellyt. Pallon lähtönopeuden kasvu jää olemattomaksi.
Jotta jännitys purkautuisi mailanpään nopeutta hyödyttäväsi, on varren annettava oieta. (Edellyttää oikeaa tekniikkaa. Niihin asioihin en puutu).
Jotta jännitys purkautuisi mailanpään nopeutta hyödyttäväsi, on varren annettava oieta.
Kuinka pitkälle?
Tästä asiasta on tälläkin forumilla taitettu peistä oikein kunnolla takavuosina. Uutta tuhannen viestin ketjua odotellessa…
Täältä löytyy suhteellisen tuore tutkimus varren käyttäytymisen tiimoilta, esim. siitä voi ihmetellä miten varsi käyttäytyy (lead / lag) ennen osumaa. https://link.springer.com/article/10.1007/s12283-019-0308-3
Vähän vanhemmassa tutkimuksessa simuloitu varren käyttäytymistä koko swingin ajan. https://people.stfx.ca/smackenz/courses/DirectedStudy/Articles/Milne%20and%20Davis%201992%20The%20role%20of%20the%20shaft%20in%20the%20golf%20swing.pdf
Näitähän voi lähteä aina haastamaan kuten akateemisessa debatissa on tapana. Jos vaan rahkeet riittää ja on intoa.
KL1
Jotta jännitys purkautuisi mailanpään nopeutta hyödyttäväsi, on varren annettava oieta.
Kuinka pitkälle?
Maalaisjärjen mukaan täysin suoraksi, muttei yhtään yli.
Maalaisjärki perustuu energiaperiaatteeseen:
lihasenergia -> jousienergia -> liike-energia (->jousienergia). Siis näin:
-varren taivuttamiseen käytetään lihasenergiaa, joka muuttuu jousienergiaksi
-varren suoristuessa jousienergia muuttuu liike-energiaksi => lavan nopeus kasvaa
-(Jos varsi ehtii taipua ennen osumaa eteenpäin, liike-energiaa muuttuu takaisin jousienergiaksi => lavan nopeus pienenee).Entä kuinka paljon maksimissaan mailanpään nopeudesta on jousivoiman tuottamaa nopeutta? Riippuu lavan ja varren massasta sekä hitausmomenteista gripin suhteen, varren jousivakiosta ja taipuman suuruudesta. Selvitin tarvittavat suureet omalle draiverilleni. Jos taipuma on 4 cm, niin pyöreästi 1 m/s, tuplataipumalla tuplasti.
P.S. En aio paneutua asiaan syvällisemmin.
Swinger?
Sitten varsinainen kysymys. Kannattaako antaa (rauta)mailan varren jännityksen purkautua niin että se lisää lavan vauhtia (mikä lisää pallon lähtönopeutta); vai ylläpitää ko jännitystä osumaan asti ja siten lyödä palloa ’kovempaa’ (vauhti + lisäjousivoima), jolloin pallo saisi myös isomman lähtönopeuden. Tuossa olisi silloin kaksi jousta vastakkain, eli onko kysymys toisin sanoen se, että kumpi jousi on jäykempi?Palaan vielä tuohon. Hyvä kysymys, jonka aiemmin luin huonosti.
Joka tapauksessa lisäjousivoima kannattaa unohtaa. Eihän se puolen millisekunnin aikana ehdi antamaan lisävauhtia eikä lisämetrejä nimeksikään. Kyse on siis vain siitä, kumpi vaihtoehdoista antaa suuremman mailanpään nopeuden. Mailanpään nopeus ratkaisee.
Jos tuota laskennallisesti haluaisi tarkastella, pitäisi ensin tietää kuinka aikaisin release alkaa ja mikä silloin on mailanpään kiihtyvyys, tai kuinka paljon varsi downswingin aikana enimmillään taipuu.
Edellisessä viestissäni päädyin omaa draiveriani koskien karheahkoilla laskemilla ja suht. epätarkoilla mittauksilla siihen, että 4 cm taipumalla lisänopeus on tai voisi olla n. 1 m/s ja riippuisi lineaarisesti varren taipumasta. En kuitenkaan tiedä paljonko se todellisuudessa taipuu, eikä aavistustakaan siitä, kuinka paljon ammattilaisten tai klubipelaajien varret alaslyönnissä taipuvat. Saisiko vinkkiä/löytyisikö linkkiä?
NimetönPG:tä kompaten, pikku vertauskuva
”jousivoima”:han on vain potentiaalia, vähän kuin takanpäälle lattialta nostettu kivi sisältää potentiaalienergiaa jonka nostaja siihen lisäsi. Kiven koskettaminen golfpallolla ei lisää pallon nopeutta, mutta jos kiven tiputtaa sopivasti golfpalloon niin jotain saattaa tapahtua.Tässä on monta hyvää ajatusta ehtiny tulla, mutta en niitä kaikkia varmaan ehdi erikseen kommentoida. Pari ajatusta kuitenkin – ja sitten yksi varsinainen asiakin mutta se tulee eri viestiin…
badgrip
Jos joku osaisi lyödä toistuvasti 10% paremmalla smashillä se varmaan tiedettäisiin.Tuli mieleen että se varmaan tiedetäänkin. Tour-prot lyö eri pituuksille ja eri lentokaarilla, joten se joukko lyö varmaan palloa eri tavalla kuin me muut. Voi olla että tuo tulee pelkästään isommista mailan nopeuksista, tai sitten siinä on mukana muutakin. Jos joku asia on ikiliikkuja, niin se on nää spekuloinnit ja tutkimukset mistä ero johtuu…
ArnoldPalmerille taas kiitos hyvistä linkeistä, luin mielenkiinnolla ja erityisesti huomioin noi vitoshandarin ja siitä parempien keskinäisten lyöntien erilaisuuden, ei ne kaikki hyvätkään samalla tavalla lyö. Huomasin myös ne varren taipumat siinä toisessa studyssä… Samaten se smash factor muistutus on hyvä huomio, varmaan tärkeämpi asia kuin useimmat meistä muistaa itseään siitä muistuttaa. En noista mailanvarsista itse osaa paljoakaan sanoa, tykkään kyllä lyödä mieluummin jäykemmälle kuin letkulla; mutta en tiedä johtuuko se siitä että löysemmän tuonti osumaan sellainen että sen ajoituksen opettelu on vaikeampaa (ja laiskana en jaksaisi sitäkin alkaa opettelemaan), vaan sitä että jäykemmästä saa tarkemman palautteen käsiin osuman jälkeen?
PG
Jos toisessa esimerkissäsi mailanpään nopeuden lisäksi myös osumageometria pysyy muuttumattomana (sehän on vertailun edellytys), niin – samasta syystä kuin edellä (0,5 ms) – lähtönopeuden lisäys on mitätön.En kopioinut koko keskustelua tähän, mutta kuitenkin – olen toki samaa mieltä että vertailukelpoisuus on tärkeä asia, ja tietyllä tapaa myös edellytys muutosten arvioinnille; toisaalta itseä kiinnostaa oppia lyömään (oman tavoitteeni kannalta) paremmin, joten siltä kannalta katsottuna jos lyön eri tavalla ja sen seurauksena pallo lentää paremmin ja/tai tullessaan alas käyttäytyy hallittavammin, niin en itse asiassa välitä siitä oliko osumageometria sama vai eri – lopputulos ratkaisee. Ja, voiman käyttäminen raudoilla rekyyliä vastaan (rekyylin eri suuntia vastaan) – siis eri tavalla kuin pelkästään lyöntisuuntaan – taitaa kuulua vähän tähän kategoriaan jossa monikin asia muuttuu kerralla.
PG
Kontaktiaika on alle sadasosa silmänräpäykseen kuluvasta ajasta. Siitä syystä, jos tarkastelu kohdistuu pelaajan osuma-aikaiseen tekemiseen, niin siinä pätee: pelaajan vaikutus on käytännössä merkityksetön, olkoon mailana mikä hyvänsä.Tässä on mun mielestä pari tärkeää asiaa, johon liittyen ainakin yhtä asiaa pitänee pohtia lisää. Ensinnäkin, tarkkaavaiset lukijat varmaan huomasi että käytin tuota mailan taipumiseen liittyvää esimerkkiä yhtenä mahdollisena tapana lisätä voimaa osumaan, mutta se oli vain esimerkki. Niitä tapoja on paljon muitakin, samaten kuin lyöntejäkin ja lyöjiä on monenlaisia.
Toisekseen, varmaan lienee selvää että jos mailanpäätä kiihdytetään yhdellä tavalla esim 20-100ms ennen osumaa, ja toisella tavalla viimeiset 10-20ms ja tämä jälkimmäinen jatkuu osuman läpi [kestot ja luvut esimerkinomaisia, ei kannata ajatella niiden olevan eksakteja] – kiihdytyksen alussahan keskipakovoima ei vielä paljoa vaikuta ja osuman tienoilla vaikuttaa paljonkin joten pelaajan käyttämien voimien suunta muuttaa matkalla; vajaissa lyönneissä noi saattaa enemmän yhdistyä samaksi; ja pyrkiikö pelaaja svingissään ns pienentämään kehää vai laajentamaan sitä; jne jne – niin joka tapauksessa tuo lopun kiihdytys (ja siinä käytettävät pelaajan aikaansaamat voimat) ennen osumaa jatkuvat sellaisenaan osuman läpi. Ei siinä varsinaisen törmäyshetken ’toimilla’ mitään enää muuteta. Joten, osuma-aikainen tekeminen ei kai voikaan olla mitään muuta kuin mitä jo tehdään valmiiksi – esim kiihdytetään mailanpäätä ja siten lisätään myös mailanpään nopeutta osumaan tullessa. Eli, en ainakaan itse ole hakemassa mitään mikä tapahtuisi ’vain törmäyshetken aikana’.
Sitten – tuo ’Kontaktiaika on alle sadasosa silmänräpäykseen kuluvasta ajasta.’ Se on niin lyhyt ettei pelaaja ehdi siihen reagoimaan. Ok. Se on myös niin lyhyt että maila ehdi välittää rekyyliä tms pelaajan reagoitavaksi. Ok. Ainoa joka ehtii siihen reagoimaan on pallo itse. Tai ehkä myös mailan lavan pintamateriaali (a la COR rajoitukset säännönmukaisilla mailoilla).
Jos oikein muistan lukemani, pallo ehtii puristua osuman aikana ’up to’ 30% halkaisijastaan (60% pallon säteestä), ja palautumaan siitä osuman aikana. Isoja lukemia.
Tuossa yhdessä tutkimuksessa, jonka linkkasin aikaisemmin, oli tutkittu osuman kestoa, ja testeissä oli havaittu se, että isommilla mailanpään nopeuksilla osuman kesto lyhenee. Ei siis pitene puristuksen lisääntyessä, vaan lyhenee. Pallohan ei tiedä mikä siihen osui, ja kuinka suurella nopeudella ja/tai voimalla lapa siihen törmää, mutta se ehtii siihen kuitenkin reagoimaanm, tuon silmänräpäyksen sadasosan aikana…! Osumien kestojen ero oli tutkimuksessa yli 10%, ja sama tapahtui konsistentisti eri pallotyypeillä, joten aika isosta vaikutuksesta puhutaan.
Voisiko tuohon asiaan vaikuttaa? Hyvä kysymys.
Osittain tuohon liittyen, keskustelut maailmalla lyöntipituuksien rajoittamisesta – kyllähän noissakin jutuissa on vahvasti mukana pallon ominaisuuksien muuttaminen, joten pallon käyttäytyminen (osumassa) on ainakin jollain tavalla merkittävä asia.
Palaten asiaan – pallo ei siis tiedä miten siihen osuttiin, se vaan reagoi siihen. Mun mutu-käsitys on se, että pallon kannalta ei ole eroa tullaanko osumaan lavan nopeudella x, vai siten että lavan nopeus on x miinus jotain mutta mukana on myös lisävoimaa (a la tuettu osuma, lapaa kiihdyttävä osuma jne), joiden yhteisvaikutus on sama kuin lavan vauhdilla x. Pallo reagoi kummassakin tapauksessa samalla tavalla.
Ja, lavan osuman voimien kasvaessa, pallon jousivoima kasvaa, ja kasvaa jopa niin paljon että osuman kesto lyhenee, sen sijaan että se pitenisi (puristus ja palautuminen kestäisi pitempään).
Ja, kuten aiemmin jo puhuttiin, kun pallon jousivoima kasvaa, sen vastavoima hidastaa vastaavasti lapaa enemmän ja pallon saama vauhti kasvaa.
Näin vauhti + voima aikaansaa saman lopputuloksen kuin suurempi vauhti.
Vastaavasti, jos lavan ’tehollinen massa’ on suurempi kuin lavan massa, sillä on sama vaikutus (’mutu’ perustuen mailanpään kasvaneeseen liikemäärän vaikutukseen).
Tein muutamia harjoituslaskelmia näistä, perustuen ko tutkimuksessa havaittuihin mailanpään nopeuksiin ja osuman kestoihin eri nopeuksilla (ja siten lavan eri liikemäärillä). Omat taidot on noiden laskelmien osalta jo vähän ruostuneet, mutta ajateltavissa olevilla muutoksilla, päädyin siihen että esim smash factoren osalta muutokset olisivat prosentin tai muutaman prosentin tasolla – ei enää prosentin murto-osia. Rautamailoilla luultavasti vähän suurempi vaikutus vielä.
Tän perusteella nostaisin ainakin pohdittavaksi, että fokus pitäisi siirtää, ei siihen mikä on lavan vaikutus palloon, vaan siihen että mikä on pallon vaikutukseen lapaan… Pallon käyttäytyminen ei ole vakio.
Swinger?
Kuulisin mielelläni myös vasta-argumentteja siltä osin kun olen harhateillä.Yritän vastata pyyntöösi. Mielestäni olit edellisessä viestissäsi monessakin asiassa harhateillä, mutta myös oikeassa.
käytin tuota mailan taipumiseen liittyvää esimerkkiä yhtenä mahdollisena tapana lisätä voimaa osumaan, mutta se oli vain esimerkki.
Voima kyllä kasvaa pikkasen, mutta sen vaikutus pallon lähtönopeuteen on minimaalinen. Shankin vertaus oli osuva. Pelkässä kosketuksessa potentiaalienergia jää käyttämättä.
Ei siinä varsinaisen törmäyshetken ’toimilla’ mitään enää muuteta. Joten, osuma-aikainen tekeminen ei kai voikaan olla mitään muuta kuin mitä jo tehdään valmiiksi – esim kiihdytetään mailanpäätä ja siten lisätään myös mailanpään nopeutta osumaan tullessa.
Juuri niin. Vain ennen osumaa tuotettu mailanpään nopeus ratkaisee.
Jos oikein muistan lukemani, pallo ehtii puristua osuman aikana ’up to’ 30% halkaisijastaan (60% pallon säteestä), ja palautumaan siitä osuman aikana. Isoja lukemia.
Todella isoja lukemia ovat. Ja riippuvat siitä, kuinka suuri vauhti mailanpäällä juuri ennen osumaa on ollut. Mailanpään nopeus ratkaisee tämänkin.
Tuossa yhdessä tutkimuksessa, jonka linkkasin aikaisemmin, oli tutkittu osuman kestoa, ja testeissä oli havaittu se, että isommilla mailanpään nopeuksilla osuman kesto lyhenee. Ei siis pitene puristuksen lisääntyessä, vaan lyhenee. Pallohan ei tiedä mikä siihen osui, ja kuinka suurella nopeudella ja/tai voimalla lapa siihen törmää, mutta se ehtii siihen kuitenkin reagoimaanm, tuon silmänräpäyksen sadasosan aikana…! Osumien kestojen ero oli tutkimuksessa yli 10%, ja sama tapahtui konsistentisti eri pallotyypeillä, joten aika isosta vaikutuksesta puhutaan.
Kyllä. Lyhyenkin hetken aikana voi tapahtua isoja asioita, kunhan vain mailanpäälle on saatu isosti nopeutta. Muuten, miten arvelet pallon lähtönopeuden muuttuvan, jos osuman kesto putoaa 10%?
Voisiko tuohon asiaan vaikuttaa? Hyvä kysymys.
Tietysti voidaan vaikuttaa: lisäämällä tai vähentämällä mailanpään nopeutta. Mailanpään nopeus ratkaisee.
Osittain tuohon liittyen, keskustelut maailmalla lyöntipituuksien rajoittamisesta – kyllähän noissakin jutuissa on vahvasti mukana pallon ominaisuuksien muuttaminen, joten pallon käyttäytyminen (osumassa) on ainakin jollain tavalla merkittävä asia.
Myös ominaisuuksiltaan muutetut uudet pallot lentävät suuremmilla mailanpään nopeuksilla pitemmälle kuin pienemmillä nopeuksilla. Mailanpään nopeus ratkaisee.
Palaten asiaan – pallo ei siis tiedä miten siihen osuttiin, se vaan reagoi siihen. Mun mutu-käsitys on se, että pallon kannalta ei ole eroa tullaanko osumaan lavan nopeudella x, vai siten että lavan nopeus on x miinus jotain mutta mukana on myös lisävoimaa (a la tuettu osuma, lapaa kiihdyttävä osuma jne), joiden yhteisvaikutus on sama kuin lavan vauhdilla x. Pallo reagoi kummassakin tapauksessa samalla tavalla.
Eli lisävoimat vaikuttavat vasta osumassa. (Ennen osumaahan ne lisäisivät mailanpään nopeutta, jolloin tuollaista vertailua ei voisi tehdä).
Luulin, että olit jo ymmärtänyt sen, että pelaajan aikaansaamat ja osuma-aikana vaikuttavat voimat – olkoonpa niiden nimet mitkä hyvänsä – ovat niin pieniä mailanpään nopeuden tuottamaan voimaan verrattuna, että niillä ei juurikaan ole merkitystä.
Ja, lavan osuman voimien kasvaessa, pallon jousivoima kasvaa, ja kasvaa jopa niin paljon että osuman kesto lyhenee, sen sijaan että se pitenisi (puristus ja palautuminen kestäisi pitempään).
Ks. edellinen kommentti.
Ja, kuten aiemmin jo puhuttiin, kun pallon jousivoima kasvaa, sen vastavoima hidastaa vastaavasti lapaa enemmän ja pallon saama vauhti kasvaa.
Ks. edellistä edellinen kommentti.
Näin vauhti + voima aikaansaa saman lopputuloksen kuin suurempi vauhti.
Ks. edellistä edellistä edellinen kommnentti.
Vastaavasti, jos lavan ’tehollinen massa’ on suurempi kuin lavan massa, sillä on sama vaikutus (’mutu’ perustuen mailanpään kasvaneeseen liikemäärän vaikutukseen).
Jos se on suurempi, niin se on kaikissa lyönneissä suurempi riippumatta siitä, miten lyödään. Ei se mikään lyöntikohtainen muuttuja olisi. Siinä toisessa ketjussa otin tuon termin käyttöön, koska vielä silloin näytti siltä, että lavan massan lisäksi osa varren massastakin tulisi ottaa mukaan liikemäärätarkasteluun. Lisätietojen valossa nyt ei enää siltä näytä, mutta mahdollista se toki on.
Swinger?: – en ole millään erityisellä asialla tässä, en ole ’alalla’, en yritä svingiohjeita antaa, en kuulu mihinkään koulukuntaan etc; olen vain asiasta kiinnostunut harrastaja, ja omia ajatuksiani tässä kirjoittelen – se on itsellä joskus hyvä tapa vähän myös selkeyttää niitä.
Uskon, että ajatuksesi selkeytyvät, jos siirrät fokuksen vähäksi aikaa palloon. Esim. piirrä vapaakappalekuvio, johon merkitset kaikki osumassa palloon vaikuttavat voimat seuraavilla lähtötiedoilla:
mclub=200g,
mball=46g,
COR= 0,795,
vclub=100 mph => vball = 146 mph,
aclub = 400 m/s^2 (iso) = lavan kiihtyvyys ennen osumaa =>
lavan kiihtyvyys osumassa 325 m/s^2 (koskee myös palloa) =>
voima osumassa = 80 N, josta palloa kiihdyttävä voima =15 N ja lapaa kiihdyttävä 65 N.
Swetariosuma ja hyvä osumageometria. Draiverilyönti.Vapaakappalekuvioon tulee siis vain kaksi samansuuntaista voimaa:
1) osuma-aikainen törmäysvoima pallolle, keskimäärin 6000 N
2) osuma-aikaisen kiihdytyksen (325 m/s^2) tuottama voima pallolle 15 NKuvaa voimavektoreita nuolilla, joiden pituus ilmaisee voiman suuruuden. Kuvio mahtuu A4-arkille, jos 30 N vastaa 1 mm pituutta. Törmäysvoiman pituudeksi tulee siis 20 cm ja kiihdytysvoiman pituudeksi puoli millimetriä.
(Huomautus: viestissä 3.2.2021 esitin tarkemman kaavan, joka ottaa huomioon myös pallon jousivoiman. Tätä kaavaa soveltaen pallon kiihtyvyydeksi tulee 437m/s^2 ja vastaavaksi voimaksi 20 N, jonka suuruutta kuvaisi O,7 mm pitkä nuoli. Ei siis oleellista eroa.)
Tiedosta, että muut voimat, jotka ennen osumaa olivat mailanpään nopeutta tuottamassa, eivät osumassa enää vaikuta. Eivät myöskään ne voimat, joita osuman jälkeen muodossa tai toisessa jossakin esiintyy. Nehän eivät vaikuta palloon. Osumassa on siis vain nämä kaksi voimaa – tai oikeastaan vain yksi. (Toisella ei ole pallon lähtönopeuden kannalta käytännön merkitystä).
Raudoilla ei ole oleellista eroa, laskut vaan vähän hankalampia ja voimat pienempiä.
Jos siis mahdollisimman pitkälle haluaa lyödä, kannattaa tuottaa mailanpäälle mahdollisimman suuri nopeus optimaalisella osumageometrialla. Millä tekniikalla mailanpää saa eniten kyytiä? Tärkeä asia, mutta siihen en ota vieläkään kantaa. Tapoja on monia, yhtä oikeata tapaa ei ole, sanovat proot. Helppo uskoa.
paitsi se lähtönopeus niin myös lentorata ja alastulo on kiinnostavia asioita.
Siitä voisi jatkaa.
P.S.
Nimimerkki PeWin kertoi aiemmin oman swinginsä tekniikasta, johon selvästi itse uskoi. Minäkin uskon, että tuo tekniikka on hyvä PeWinille. Sopii varmaan monelle muullekin. Swingerkin luottaa omaan tekimiseensä – hyvä perusta swingin onnistumiselle. Fysiikkaan pohjautuvat perustelut menevät kuitenkin monesti metsään. Mutta mitä siitä, jos svingi toimii. Siitä vaan.Voi olla että tässä keskustelussa päädytään klassiseen lopputulokseen – ollaan samaa mieltä että ollaan eri mieltä. Tosin, omalta osaltani kyse on enemmänkin tutkivasta epäilystä kuin mielipiteestä.
PG
Muuten, miten arvelet pallon lähtönopeuden muuttuvan, jos osuman kesto putoaa 10%?Tässä kontekstissa, kasvaa paljon.
PG
Swinger?
Palaten asiaan – pallo ei siis tiedä miten siihen osuttiin, se vaan reagoi siihen. Mun mutu-käsitys on se, että pallon kannalta ei ole eroa tullaanko osumaan lavan nopeudella x, vai siten että lavan nopeus on x miinus jotain mutta mukana on myös lisävoimaa (a la tuettu osuma, lapaa kiihdyttävä osuma jne), joiden yhteisvaikutus on sama kuin lavan vauhdilla x. Pallo reagoi kummassakin tapauksessa samalla tavalla.Eli lisävoimat vaikuttavat vasta osumassa.
Tässä kontekstissa, eli mitä pallo tekee tai aikaansaa osuman aikana, juuri näin. Pallo on paikallaan törmäyshetkeen asti, joten pallo voi vain reagoida osuman aikana.
PG
Luulin, että olit jo ymmärtänyt sen, että pelaajan aikaansaamat ja osuma-aikana vaikuttavat voimat – olkoonpa niiden nimet mitkä hyvänsä – ovat niin pieniä mailanpään nopeuden tuottamaan voimaan verrattuna, että niillä ei juurikaan ole merkitystä.Tuo on mulle vielä kaksijakoinen juttu – mailanpään lisäkiihtyyvyden osuman keston aikana osalta tilanne on selvä (ei merkittävää vaikutusta), mutta pallon tuottamien voimien osalta ei ole, ainakaan vielä. Jätän sille ajatukselle vielä (kasvavaa) elintilaa.
Viittaan myös esim tähän seuraavaan:
PG
Swinger?
1) jos palloa puristaa isommalla voimalla, se puristuu enemmän. Oikein vai väärin?
4) jos pallo on puristunut enemmän, sen jousivoima antaa palautuessaan isomman potkun lavalle. Oikein vai väärin?
6) jos pallo palautuessaan puristuksesta antaa isomman potkun, lapa hidastuu edemmän. Oikein tai väärin?Oikein 1) ja 4)
Oikein 6)Mun ajatuksissa toi osumahetken lyheneminen mailanpään vauhdin kasvaessa kertoo että lisävoima johtaa siihen että pallon antaa ja saa lisäpotkua, ja pallohan ei tiedä tuliko lisävoima lavan lisävauhdista vai jostain muusta voimasta.
PG
Vapaakappalekuvioon tulee siis vain kaksi samansuuntaista voimaa:
1) osuma-aikainen törmäysvoima pallolle, keskimäärin 6000 N
2) osuma-aikaisen kiihdytyksen (325 m/s^2) tuottama voima pallolle 15 NMulla oli mielessä ehkäpä näin
1) osuma-aikainen törmäysvoima pallolle, keskimäärin 6000 N
2) pelaajan osuma-aikainen voima – pallon lisärekyyli (jousivoima) 60 NEli, prosentin luokkaa driverilla. Aina pieni siis, mutta driverin osalta en ole muuta ajatellutkaan. Rautalyöntien osalta pelaaja pystyy tuottamaan erikseen voimaa enemmän loft-kulmaa vasten joten niissä vaikutus voi olla selvästi suurempi – eli lisävoima kohdistuisi enemmän (suhteessa) myös varren suuntaan eikä pelkästään lyöntisuuntaan – jolloin prosentiaalinen vaikutus on jo mahdollisesti selvästi isompi.
PG
Swinger?
Vastaavasti, jos lavan ’tehollinen massa’ on suurempi kuin lavan massa, sillä on sama vaikutus (’mutu’ perustuen mailanpään kasvaneeseen liikemäärän vaikutukseen).Jos se on suurempi, niin se on kaikissa lyönneissä suurempi riippumatta siitä, miten lyödään. Ei se mikään lyöntikohtainen muuttuja olisi.
Mulla on taas orastava ajatus että pystyisin tuohon lyöntikohtaisesti vaikuttamaan. Varren viimeisellä kolmanneksella tai neljänneksellä voi olla erilainen vaikutus riippuen miten lyödään, ja tuon vaikutus (vaikkakin kuulostaa pieneltä) voi olla jokunen prosentti tai prosentin osa lisää.
PG
Nimimerkki pewin kertoi aiemmin oman swinginsä tekniikasta, johon selvästi itse uskoi. Minäkin uskon, että tuo tekniikka on hyvä pewinille. Sopii varmaan monelle muullekin. Swingerkin luottaa omaan tekimiseensä – hyvä perusta swingin onnistumiselle. Fysiikkaan pohjautuvat perustelut menevät kuitenkin monesti metsään. Mutta mitä siitä, jos svingi toimii. Siitä vaan.Erinomainen yhteenveto koko jutusta – kaksi peukkua ja leveä hymiö päälle!
paitsi se lähtönopeus niin myös lentorata ja alastulo on kiinnostavia asioita.
Törmäyslaskut perustuvat liikemääriin, lentoratalaskut voimiin. Vinon heittoliikkeen kaavoissa otetaan huomioon ainoastaan maan vetovoima. Siksi niiden avulla lasketut lentoradat eivät paljon muistuta golfpallon lentorataa, ei ainakaan suurilla nopeuksilla – paitsi kuussa. Toistaiseksi kuussa ei ole golfkenttiä. Pidetään siis jalat maassa.
Ilmalennossa golfpalloon vaikuttaa maan vetovoiman lisäksi myös ilmanvastus ja alakierteestä johtuva nostovoima. Molemmat riippuvat ilmantiheydestä, joka puolestaan määräytyy ilman lämpötilan ja -paineen perusteella. Ilmanvastus on suoraan verrannollinen nopeuden neliöön ja on aina radan tangentin suuntainen. Nostovoima on kohtisuorassa radan tangenttia vastaan. Sen suuruus riippuu pallon
etenemisnopeudesta ja pyörimisnopeudesta. Ratkaisun lähtökohtana on em. voimien kiihtyvyyksiin perustuva toisen kertaluvun differentiaaliyhtälöryhmä. Omassa ratkaisussani 26 vuotta sitten lähdin liikkeelle differentiaaliyhtälöparistad²x/dt² = – k1*dx/dt – k2*dy/dt
d²y/dt² = – g – k1*dy/dt + k2*dx/dt
jossa d²x/dt² on pallon hetkellinen kiihtyvyys vaakasuuntaan ja d²y/dt² kiihtyvyys pystysuuntaan (molemmat ’matkan toisia derivaattoja ajan suhteen’). Termit dx/dt ja dy/dt puolestaan tarkoittavat pallon hetkellisiä x- ja y- suuntaisia nopeuksia (aikaderivaatat x- ja y- suuntiin). Kerroin k1 on ilmanvastukseen ja k2 alakierteeseen liittyvä kerroin ja g putoamiskiihtyvyys.
Diff.yht.parin ratkasuna saadaan lentoradan x- ja y- koordinaatit ajan t funktiona. Integroinnit poikivat lisää kertoimia c1, c2, d1 ja d2 riippuen osin toinen toistaan, (esim. d2 = 1/k2*[d1*k1 – g – vo*(k1*sin(alfa) – k2*cos(alfa))]). Kulma alfa = arctan[(dy/dt)/(dx/dt)]). (Muuttuu koko ajan).
[Todennäköisesti kukaan ei enää ole jaksanut lukea näin pitkälle, joten voin paljastaa, että lähtöyhtälöissäni ilmanvastus riippuu vain pallon hetkellisestä nopeudesta, ei nopeuden neliöstä. Samalla muistutan itselleni, miksi näin tein. Syy oli se, että nopeuden neliöstä riippuva diff.yht.pari ei ole ratkaistavissa suljetussa muodossa (jolla saataisiin selvät kaavat x= x(t), y=y(t)). Numeerinen ratkaisu nopeuden neliötä käyttäen ei ole matemaattisesti vaikea. Itseäni kiinnosti kuitenkin saada kasaan vinon heittoliikkeen kaavoihin verrattavat kaavat x=x(t), y=y(t). Ilmanvastus on mallissani siis liian pieni, eikä näin ollen lentoradan muoto täysin oikea.]
Aiemmin Swinger sovelsi vinon heittoliikkeen kaavoja verratessaan lyöntien pituuksia lähtönopeuksilla 67,4 m/s, 68,8 m/s ja 70,6 m lähtökulman ollessa 15°. Pituudet olivat vastaavasti 231 m, 241 m ja 254 m. Ok. Ne eivät tietenkään ole oikeat (eikä Swinger niin väittänytkään), vain suuntaa-antavat. Lentoradat ovat paraabeleja, joten lakikorkeudet 14 m, 16 m ja 17 m sijoittuvat radan puoleen väliin. Tulokulma maahan on sama kuin lähtökulma.
Omat kaavani antavat näillä lähtöarvoilla vastaavasti 231 m, 236 m ja 241 m, kun ilman lämpötila on 20° C ja ilman paine 760 Hgmm. (Kymmenen asteen lämpötilan alentaminen tai 20 Hgmm paineen nostaminen lyhentävät lyönnin pituutta kaksi kolme metriä). Maksimikorkeus saavutetaan, kun n. kolmannes lentomatkasta on jäljellä. Lakikorkeudet ovat 29 m, 30 m ja 32 m – siis tuplasti se, mitä vinon heittoliikkeen kaavat antavat. Tulokulmat maahan lähtökulmalla 15 astetta ovat 40°, 41° ja 42° (heittoliikkeen kaavalla 15°). Ei nämäkään arvot oikeita ole, mutta huomattavasti lähempänä totuutta, kuin vinon heittoliikkeen antamat.
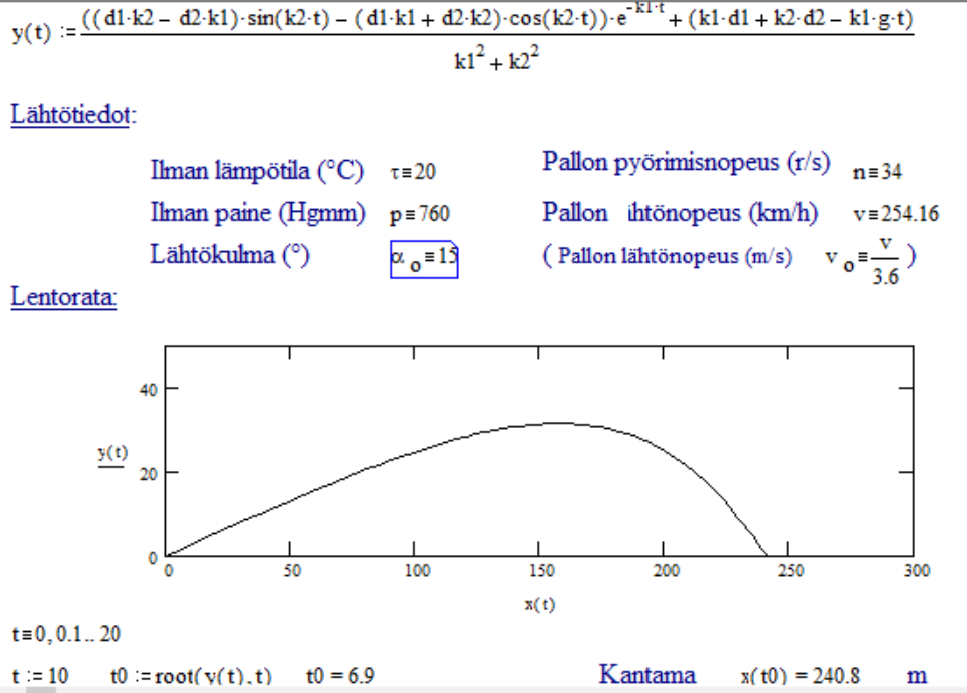
Valitettavasti näillä tiedoilla kenenkään peli ei parane, mutta tulipahan pieni loppukevennys vastapainona lähes ylivoimaisen vaikeiksi käyneille liikemäärälaskuille..
NimetönPG:n loppukevennykseen vielä loppuraskaannus(?)
Tämä noin 200 viestin ketju käsitteli etupäässää sitä, mitä tapahtuu osumassa liikemäärien suhteen. Kun aletaan miettimään miten pallo sitten itseasiassa lentää, niin mennään yhtä tai kahta suuruusluokkaa vaikeamman asian pariin, eli aeromystiikkaan.Tässä esimerkiksi alustusta siitä, että magnus- efekti ei välttämättä kaikilla reynoldseilla nostakaan palloa.
https://link.springer.com/article/10.1007/s12283-020-0318-1Lueskelin Penneriä ao pätkän.
Pappa Tykki
Suosikkilähteeni Penner (s.145-6) kertoo pallomalleista (normaaliosumassa):
– yhdistelmä epälineaarisia elastisia elementtejä ja dissipatiivisiä elementtejä vaikuttamassa pistemäiseen massaan
– yksinkertaisimmassa kaksiparametrimallissa (Cochran, 1999) on Hertsinen jousi (voima verrannollinen kokoonpuristuman potenssiin 3/2), joka on homogeeneisen kokoonpuristuvan pallon teoreettinen malli; tämän rinnalla on dissipatiivinen elementti, jonka voima on verrannollinen kokoonpuristumisen nopeuteen kertaa kokoonpuristuman neliöjuuri
– Cochrainin mallissa COR laskee mailanpään nopeuden kasvaessa (sopusoinnussa kokeellisetne tulosten kanssa)
– Johnson ja Lieberman (1994, 1996) ovat esittäneet viisiparametrisen mallin, jonka kuva ja yhtälöt PennerissäHuomasin että Penner (v. 2002) referoi myös tuota toista tutkimusta mihin viittasin (Robert et al, 2001).
Jos tuon oikein ymmärrän, niin se oikeastaan yksinkertaistaa ainakin omaa ajattelua asiasta. Jos pystyn osumassa puristamaan palloa lisävoimalla litistymään enemmän, niin ko pallon Hertsinen jousivoima lisääntyy potenssiin 3/2. Mikä sitten potkaisee lapaa vastaavasti enemmän, se hidastuu osumassa enemmän ja smash factor kasvaa – ja pallo saa isomman vauhdin. Liikemäärien ja voimien osalta en keksi tuossa ristiriitaa.
Suuruusluokkina, jos täysvauhtisessa lyönnissä voimat on jo 6000N luokkaan, en usko että pystyn lisävoimalla (esim aiemmin mainittu 60N) merkittävästi palloa lisää vielä puristamaan, joten mailanpään vauhti dominoi tilannetta.
Vajaassa lyönnissä taas voimat on 1000N luokkaa, ja siinä 60N lisävoima olisi jo merkittävä lisä, varsinkin kun lisäpuristuksen määrä nostaa vastavoimaa potenssiin 3/2, joten prosentteina tuosta tulee jo sellainen että se näkyy. Tämä vastaa myös omaa tuntumaa – pallo lähtee kovempaa jos painan/tuotan lisävoimaa tuollaisessa lyönnissä (osuman tulevaa) rekyyliä vastaan.
Pystynkö erottamaan mikä osa lisävoimasta johtaa jo ennen osumaa lisävauhtiin ja mikä pallon lisäpuristumiseen. Luultavasti en, koska osuman kesto on niin lyhyt ja sama voima vaikuttaa molempiin. Sen sijaan luulisin tunnistavani (nyttemmin) kyllä palautteen mikä tulee käsiin heti osumaan jälkeen ja tietysti myös pallon lentorata näkyy toisena palautteena – osuma on erilainen ’paineistetussa lyönnissä’ vs ’läpilaskijan lyönnissä’. Molemmista on jo kokemusta.
Mutta, jos nyt olen yhtään ymmärtänyt ko fysiikkaa, niin ainakin omalta kohdaltani olen saanut selityksen osuman rekyylin tunnistamisen merkitykselle ja sitä vastaan lisävoimalla lyömiselle. Ei muuta kuin hallille jatkamaan.
NimetönVajaassa lyönnissä taas voimat on 1000N luokkaa, ja siinä 60N lisävoima olisi jo merkittävä lisä, varsinkin kun lisäpuristuksen määrä nostaa vastavoimaa potenssiin 3/2, joten prosentteina tuosta tulee jo sellainen että se näkyy.
Ehkä tarkoitit jotain muuta tässä, mutta aloin miettimään että jos vajaaseen lyöntiin haluaa lisävoimaa niin eikös silloin vaan kannattaisi lyödä vähemmän vajaa lyönti?
Ei muuta kuin hallille jatkamaan.
Kyllä!
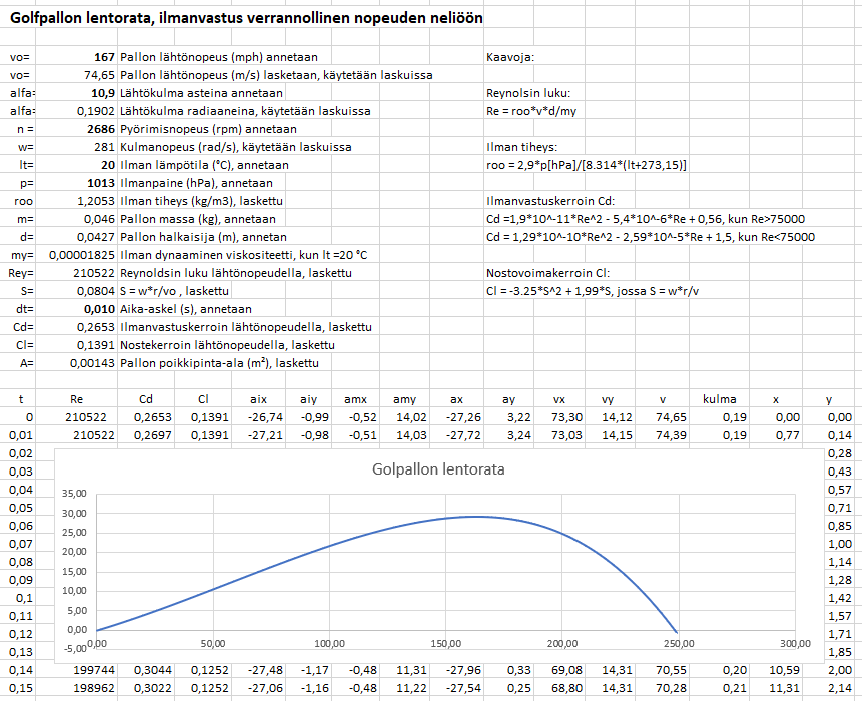
Tässä vielä uudelleen loppuraskaannuksen beetta-versio toteutettuna numeerisesti Excelillä. (Edellinen viesti hävisi vahingossa bittiavaruuteen). Kuvan esittämässä lyönnissä ilman lämpötila on 20 °C ja -paine 1013 hPa => kantama 248 m. Jos lämpötila muuttuu 1013 hPa:n paineessa + – 10 °C, niin lyönnin pituus muuttuu + – 3 m. Jos paine muuttuu 20 °C:ssa + – 20 hPa, niin pituus muuttuu – + 2 m. Siis tämän mallin mukaan. Vastaako se todellisuutta? Ei se ole mitenkään varmaa. Testaillaan vielä. Käänteinen noste kyllä toteutuu, johtuen yksinkertaisesti tutkijoiden havaitsemasta ilmiöstä ja heidän kaavastaan
Cl = -3.25*S^2 + 1,99*S, jossa S = w*r/v.
Jos w/v>28,68, niin kaavan perusteella nostovoiman pitäisi mennä negatiiviseksi! Ja menee kans..
Shank
Ehkä tarkoitit jotain muuta tässä, mutta aloin miettimään että jos vajaaseen lyöntiin haluaa lisävoimaa niin eikös silloin vaan kannattaisi lyödä vähemmän vajaa lyönti?Joo, totta, lyödä voi monella tapaa. Itselleni sopii toi voiman säätely ja kohdistaminen rekyyliä vastaan, sillä tuntuu saavan helpommalla paremman kontrollin lyönnin pituudesta (menee pitemmälle hallitummin) ja pallon alastulosta. Saan myös parempia osumia lyhyemmällä svingillä, mikä sekin auttaa omaa tekemistä. Nää on toki siis vain omia preferenssejä, jotka lähti alunperin liikkeelle tosta aiemmin mainitusta ’lyö kuin superpalloa’. Ei se ihan niinkään mee, mutta tekeminen meni tuohon suuntaan ja muuttui helpommaksi.
Mielenkiintoista kuinka tämäkin ketju (näin talviolosuhteissa) lähti lapasesta alkuperäisen aiheen ulkopuolelle, mutta onhan tällä saitilla ollut muitakin OB ketjuja. Tämä golfin peluu kaiken kaikkiaan ”ei periaatteessa” ole mitään rakettitiedettä (”rocket science”), vaan lähempänä John Dalyn periaatetta: lyön palloa niin lujaa kuin pystyn ja jos löydän sen, niin lyön uudelleen”.
Täällä muissa keskuteluissa puhutaan että Bryson DeChambeau olisi ”hullu tiedemies”. Omasta mielestäni hän ei nyt varsinaisesti täytä tiedemiehen määritelmää, mutta tekee sisukkkaasti empiirisiä testejä rangella ja kentällä ”yritys ja erehdys” periaatteella, ja tuntuu pärjäävän omalla vahvuusalueellaan.
Omasta mielestäni nimimerkki ”PG” on oikea tiedemies. Teitkö PG jopa väitöskirjasi golf-lyönnin mekaniikasta?
Itse en ole jaksanut enää kahlata kaikkia viestejä lävitse ja olen samaa mieltä kuin ”Shank”, että olisi hyvä jos ”Swinger?” ja ”PG” avaisivat tarvittaessa uuden ketjun. Kiitos mielenkiintoisesta keskustelusta joka tapauksessa.
”I väntan för bättre tider” eli kenttien avautumista odotellessa.Mc Tavis
Mielenkiintoista kuinka tämäkin ketju (näin talviolosuhteissa) lähti lapasesta alkuperäisen aiheen ulkopuolelleTalvellahan on hyvää aikaa näitä juttu resonoida… Joo ajatus oli ihmetellä noita voimia osumassa, mutta sitten tulikin pitkä keskustelu onko niistä mitään hyötyä ylipäätään (’vain vauhti ratkaisee’). Johonkin lopputulokseen pääsin ainakin itse sen suhteen (’on/voi olla’). Niistä voimista taas ei paljoa juttua syntyny, joten mun puolesta voidaan hyvin lopettaa tai antaa mennä OB vapaasti, seuraavaa kautta odotellessa.
Mielenkiintoista kuinka tämäkin ketju (näin talviolosuhteissa) lähti lapasesta alkuperäisen aiheen ulkopuolelle, mutta onhan tällä saitilla ollut muitakin OB ketjuja.
Omasta mielestäni tämä ketju moneen muuhun ketjuun verrattuna on pysynyt lapasessa hyvin. Itse aioin päättää juttuni jo ’loppukevennykseen’, mutta valitettavasti tuli vielä tuo ’loppuraskaannus’. Shankin syy 😉 Tosin jo ketjun avauksessa Swinger mainitsi lyönnin pituuden – osana aihetta, ymmärsin – sekä myöhemmin että lentoratakin kiinnostaa. Ei nuokaan aiheet siis ihan OB:tä olisi olleet.
Tämä golfin peluu kaiken kaikkiaan ”ei periaatteessa” ole mitään rakettitiedettä (”rocket science”), vaan lähempänä John Dalyn periaatetta: lyön palloa niin lujaa kuin pystyn ja jos löydän sen, niin lyön uudelleen”.
Täysin samaa mieltä. (Tosin on muistettava, että tämän ketjun aiheena ei ollut ’golfin peluu’, vaan ’voimaa osumaan’. Voima = massa x kiihtyvyys. Laskelmani ovat mielipiteideni perusteluja. Sanallinen selittely ei aina riitä.)
Täällä muissa keskuteluissa puhutaan että Bryson DeChambeau olisi ”hullu tiedemies”. Omasta mielestäni hän ei nyt varsinaisesti täytä tiedemiehen määritelmää, mutta tekee sisukkkaasti empiirisiä testejä rangella ja kentällä ”yritys ja erehdys” periaatteella, ja tuntuu pärjäävän omalla vahvuusalueellaan.
Tuosta minulla on ollut täysin päinvastainen käsitys – tällainen:
Bryson DeChambeau – Moe Normanin jalanjäljillä | Spikebar
DeChambeau suhtautuu tekemisiinsä kentällä ja sen ulkopuolella harvinaisen analyyttisesti. Kiinnostus tämän maailman lainalaisuuksiin näkyy myös hänen yliopisto-opintojensa pääaineessa, joka on fysiikka.Vuonna 2011 DeChambeau ryhtyi pohtimaan omaa golfsvingiään juuri fysiikan ja mekaniikan lakien kautta. Olisiko kaikki mahdollista tehdä tavalla, joka laittaisi mutkat suoriksi?
Onko Bryson oikeasti valmistunut jostakin opinahjosta fyysikoksi vai ovatko hänen opintonsa samaa laajuutta kuin kirjailija Miika Nousiaisen kaksi kesken jäänyttä sosiologian kurssia?
-
JulkaisijaArtikkelit
Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros


