Hakutulokset: "mailanpään hidastuminen"

[PG]

ts kirjoitti: (1.5.2011 10:28:09)

PG kirjoitti: (1.5.2011 10:04:22)
[

Outoja kirjoittelet (mm. heilurimalli). Outoja väität (mm. suorassa kulkevan lavan kannalla ja kärjellä on sama nopeus). Kaari on kaari ja se näkyy kaarena myös kaikissa projektioissa paitsi kaaren tasoa vastaan kohtisuorissa olevissa projektioissa. Niistä tuskin on kysymys. Sitä paitsi et puhu mistään projektiosta, vaan esim., että ’selkeästi todetaan lavan liikkuvan suoraan haluttuun suuntaan’.

Noista mainitsemistasi mittaustuloksista olen kiinnostunut.

Luetko sät tätä ketjua lainkaan? Ei tuosta hirveen montaa viestiä ole kun selkeän kuvan laitoin.

Ja noin 30 kertaa olen koittanut saada sinut nimenomaan ymmärtämään, että asiaa pitää tuolta osin tarkastella tietyn projektion suhteen. Niitä viestejä on todellakin useita, mutta jostain syystä et ole halunnut viestin menevän perille. Ei edes se perusasia, että se nyt vaan ei ole kaari, vaikka laskukoneesi sitä sellaiseksi luuleekin.

Samoin et ole huomannut ilmeisesti kysymystäni lavan ja käsien kulkeman reitin matkallisesta erosta. Vai onko se liian vaikea kysymys, kun vastausta et le pystynyt antamaan?

Mä voin kertoa sulle yhden salaisuuden kunhan et levitä sitä yhtään eteenpäin: Jokaisen hyvän pelaajan kädet on liikkeessä ylläviistoon jo pitkän matkaa ennen osumaa. Silti lapa voi olla laskussa tai nousussa, vahventua tai heikentyä, aueta tai sulkeutua osuma-alueella.
Ratkaise nyt tuo yhtälö ensin itsellesi ja mieti sitten mihin muuhun laskelmissasi se voi vaikuttaa.

Samaan aikaan lavalla on reilusti enemmän nopeutta kuin käsillä, mutta kehällä se ei saavuta niitä vielä pitkään aikaan, puhumattakaan että ohittaisi ne. Lisäksi niillä on täysin eri kulkusuunta myös kohteeseen nähden.

Eli ihan huoletta saat työntää nuo laskelmasi johonkin pimeään paikkaan, koska niistä puuttuu lähes täyden vapausasteen nivel ranteiden kohdalta, sekä myös varsin suuren vapausasteen muita niveliä tuolta sisempää ja ylempää järjestelmästä. Se ei todellakaan ole around the fixed hub vaan kaukana siitä.

Noin 30 kertaa olen yrittänyt saada sinut ymmärtämään, että svingiasioilla ei ole mitään tekemistä tämän asian kanssa. Ongelma selviää puhtaasti kinemaattisella tarkastelulla. Mailan tilalla voisi olla vaikka keppi ja svingin tilalla liike, joka siirtää kepin uuteen asemaan. Nopeuksillakaan ei juuri ole väliä, kunhan tiedetään päätepisteiden kulkema matka. (Tarkastelujakson aikainen epätasainen nopeus toki vaikuttaisi jonkin verran sen radan muotoon, jota grippipää kulkee). Koordinaatiston valinta on vapaa. x-akseli voi suuntautua paitsi kohteen suuntaan, myös siitä sivulle, ylös tai alas. Toinen pää valitaan kulkemaan x-akselin suuntaan, toinen pää menee sinne, mitä laskelmat näyttävät. Jos golflyönnistä on kyse, on aivan sama onko pelaaja hyvä vai huono, ovatko kädet menossa ennen tarkastelutilannetta ylös vai alas, ovatko ne edessä vai takana, lapa nousussa vai laskussa. Tarkastelutilanteessa lavan oletetaan menevän suoraan. Laskelman perusteella arvioidaan, onko homma käytännössä mahdollinen.

Laskelmat näyttävät pahasti siltä, että vaikka lavan suoraan kulkeminen on teoriassa mahdollista, niin käytännössä se ei ole.

[ts]

B kirjoitti: (1.5.2011 16:49:14)

Vanhat opetukset faden ja drawn lyömiseksi olivat myös ilmeisen virheellisiä. Moni oppi niiden avulla taivuttamaan palloa oikeaan ja vasempaan ihan hyvin. Vielä useammat eivät koskaan oppineet.

Tai sitten vaan oppivat niistä huolimatta. Suurin osa oppineistakin silti väärin ja liian isolla kierteellä.

Eikä D-planessa sinänsä mitään ihmeellistä ole. Yhtäkkiä vaan tajuttiin siinä lavassa olevan loftiakin 🙂 Hauskaa on se, että nyt siellä vouhkataan otsikolla, että vanhat lentolait ei pidä paikkaansa. Ne pitävät aivan varmasti, mutta niiden yhteisvaikutusten tarkastelu on kehittynyt. Lait eivät ole kyllä muutuneet yhtään mihinkään.

[B]

Mitä välii?
Ei mitään. Matemaattis-fysikaalisesti virheellisillä väittämillä voidaan saada valmennuksellisesti ihan hyviäkin tuloksia. Tämää pätee tukivoima-ajatuksiin yhtä hyvinkuin näihinkin.
Vanhat opetukset faden ja drawn lyömiseksi olivat myös ilmeisen virheellisiä. Moni oppi niiden avulla taivuttamaan palloa oikeaan ja vasempaan ihan hyvin. Vielä useammat eivät koskaan oppineet.
Eräs blogin pitäjä ennusti, että pian tulevat vanhat gurut opettamaan New Ball Flight Laws: eja pokkana niinkuin olisi ne aina tajunnut.
Oliko Jim McLean ensimmäinen? 🙂

[B]

ts kirjoitti: (1.5.2011 12:22:12)

duffeli kirjoitti: (1.5.2011 11:31:56)
Nuo tuhansia vuosia voimassa olleet laskentakaavat ovat luonnollisesti käyttökelpoisia tänäkin päivänä. Valitettavasti niiden avulla voidaan selvittää vain suhteellisen yksinkertaisia liikekokonaisuuksia, joita ei voida suoraan verrata golfswingin tyyppiseen epälineaariseen liikkeeseen.

Jokainen kaava, josta yksikin mahdollinen muuttuja puuttuu on arvoton. Sellaista kaavaa, jossa ne kaikki olisivat huomioidut, ei pysty kukaan tuottamaan, koska liikkeet ovat varsin epälineaarisia.

Näin juuri. Yksinkertaista geometrista tarkastelua käyttäen PG yritti löytää ratkaisun kysymykseen, millä grippipään liikkeellä mailanpään ’sweetspot-piste’ liikkuu 20 cm suoraan kesken kaarevan polkunsa. Ei tuosta tarkastelusta puuttunut muuta kuin ts:ltä pyydettyjä mittausarvoja nopeuksien vektorisuunnista, jotka ts.lla ilmeisesti on kassakaapissa. Tai sitten ei.
Niilla olisi saatu laskennallisesti toivottavasti todennetuksi tuo ilmiö.

ts tarjosi graafin, jossa on kaari ja suora. Tässäkö on mittausdata ,joka kysymyksen ratkaisee.
Piirsin paperille ballograafilla kaaria sapluunalla, joka oli halkaisijaltaan n. 10 cm. vedin niihin viivottimella tangentteja. Kaaren ja suoran viivan yhtenevä osuus oli pituudeltaan n. 5mm-10mm.
silmämääräisesti kaaren tangeeraava osa oli oiennut kuin taikaiskusta.
Mitä opimme. Tuollainen ’mittausdata’ ei ratkaise juuri tätä kysymystä. Matematiikka sen ratkaisee. Siihen ei vaikuta heilurit, käsikolmiot tai muut hemputukset. Ne vaikuttavat kussakin lyönnissä mailanpään ja grippipään liikkeeseen tämän lyhyen hetken ajan, jolloin radan siis piti oieta. Oikeniko ko tapauksissa ratkeaa, kun sijoitetaan mittausarvot kaavoihin. Mittatarkkuuden puitteissa.
Manzellalla on kamera. Niin minullakin. Minäkin käytän vartalorotaatiota käsivarsikrossauksen sijaan johtoajatuksena. minäkään en usko, että yksinkertainen tuplaheiluri on hyvä svingi-ideaali.
Näillä ei ole tekemistä PG viimeisen laskelman kanssa. Uskokaa pois.

[duffeli]

Kiitos, palaan aiheeseen myöhemmin. Täytynee hieman viihdyttää perhettä…

[ts]

duffeli kirjoitti: (1.5.2011 13:03:16)
Mistä kohdasta muuten tuo käsien liikerata on tarkkaan ottaen mitattu?

Vasen ranne on tarkka mittapiste.

[duffeli]

Mistä kohdasta muuten tuo käsien liikerata on tarkkaan ottaen mitattu?

[ts]

duffeli kirjoitti: (1.5.2011 11:31:56)
Nuo tuhansia vuosia voimassa olleet laskentakaavat ovat luonnollisesti käyttökelpoisia tänäkin päivänä. Valitettavasti niiden avulla voidaan selvittää vain suhteellisen yksinkertaisia liikekokonaisuuksia, joita ei voida suoraan verrata golfswingin tyyppiseen epälineaariseen liikkeeseen.

Juuri tästä on kysymys. Golflyönti on aivan liian monimutkainen ja jatkuvasti suunnaltaan muuttuvia liikkeitä sisältävä, että sitä voitaisiin ratkoa matemaattisten kaavojen yhtälöinä. Kehät supistuvat, laajenevat, oikenevat ja jyrkkenevät jatkuvasti swingin eri vaiheissa ja lisäksi nitä on moniin suntiin, jopa vastakkaisiin, kumoten toistensa vaikutukset.

Jokainen kaava, josta yksikin mahdollinen muuttuja puuttuu on arvoton. Sellaista kaavaa, jossa ne kaikki olisivat huomioidut, ei pysty kukaan tuottamaan, koska liikkeet ovat varsin epälineaarisia.

[duffeli]

Nuo tuhansia vuosia voimassa olleet laskentakaavat ovat luonnollisesti käyttökelpoisia tänäkin päivänä. Valitettavasti niiden avulla voidaan selvittää vain suhteellisen yksinkertaisia liikekokonaisuuksia, joita ei voida suoraan verrata golfswingin tyyppiseen epälineaariseen liikkeeseen. Monesti epälineaariset mallit esitetäänkin suljetussa muodossa systeemin dynamiikkaa kuvaavien differentiaaliyhtälöiden ratkaisuna. Golfswingin kaltaisessa liikkeessä differentiaaliyhtälöitä ei kuitenkaan voida analyyttisesti ratkaista, ja sen vuoksi parametrit täytyy estimoida sovittamalla differentiaaliyhtälöistä numeerisesti laskettu ratkaisu todelliseen
havintoaineistoon. Tämän selvemmin en osaa tätä maallikkona ilmaista ja tähänkin piti jo lainata muiden lauseita. Olet PG vakuuttava matemaattisissa taidoissasi, mutta asian etenemisen kannalta olisi mukavaa jos uskoisit, että hommaa on tutkittu jo hieman aikaisemminkin. Mikäli swingin salat kyettäisiin mallintamaan noin helposti, lukisimme faktat golfkirjoista, sen sijaan että kiistelisimme tällä foorumilla tähän tapaan. Itse uskon 4D tyyppiseen sovellukseen vahvasti. Toivottavasti saatte kansainvälistä menestystä, ennen kuin joku perässähiihtäjä kerää omenat. Nimimerkillä vappusima saa pään pyörälle. 🙂

[ts]

4par kirjoitti: (1.5.2011 11:06:34)

ts kirjoitti: (30.4.2011 9:10:29)
Tai sitten mittaamalla esim lavan etäisyyttä kohdelinjasta eri vaiheissa…

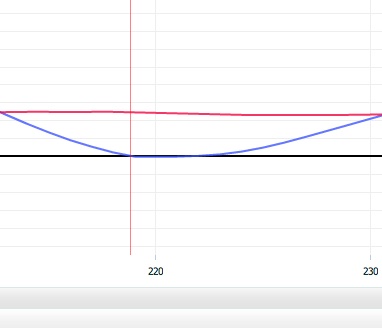
Mitä ovat kuvion kaaret/suorat:
* musta – kohdelinja (?)
* sininen – lavan kulkema kaari (?)
* punainen ?

Punainen on käsien liikerata, eli tuossa graafissa on mitattu lavan ja käsien etäisyyttä mustasta viivasta joka on siis kohdelinja. Datapankista löytyy myös mittauksia, joissa tuo punaisen linjan etäisyys mustasta on kasvussa jo punaiselle pystyviivalle (osumahetki) tullessa ja jatkaa kasvuaan siitä, vaikka lapa kulkekin varsin pitkään mustaa linjaa pitkin. Jopa pidempään kuin tuossa.

[4par]

ts kirjoitti: (30.4.2011 9:10:29)
Tai sitten mittaamalla esim lavan etäisyyttä kohdelinjasta eri vaiheissa…

Mitä ovat kuvion kaaret/suorat:
* musta – kohdelinja (?)
* sininen – lavan kulkema kaari (?)
* punainen ?

[ts]

PG kirjoitti: (1.5.2011 10:04:22)
[

Outoja kirjoittelet (mm. heilurimalli). Outoja väität (mm. suorassa kulkevan lavan kannalla ja kärjellä on sama nopeus). Kaari on kaari ja se näkyy kaarena myös kaikissa projektioissa paitsi kaaren tasoa vastaan kohtisuorissa olevissa projektioissa. Niistä tuskin on kysymys. Sitä paitsi et puhu mistään projektiosta, vaan esim., että ’selkeästi todetaan lavan liikkuvan suoraan haluttuun suuntaan’.

Noista mainitsemistasi mittaustuloksista olen kiinnostunut.

Luetko sät tätä ketjua lainkaan? Ei tuosta hirveen montaa viestiä ole kun selkeän kuvan laitoin.

Ja noin 30 kertaa olen koittanut saada sinut nimenomaan ymmärtämään, että asiaa pitää tuolta osin tarkastella tietyn projektion suhteen. Niitä viestejä on todellakin useita, mutta jostain syystä et ole halunnut viestin menevän perille. Ei edes se perusasia, että se nyt vaan ei ole kaari, vaikka laskukoneesi sitä sellaiseksi luuleekin.

Samoin et ole huomannut ilmeisesti kysymystäni lavan ja käsien kulkeman reitin matkallisesta erosta. Vai onko se liian vaikea kysymys, kun vastausta et le pystynyt antamaan?

Mä voin kertoa sulle yhden salaisuuden kunhan et levitä sitä yhtään eteenpäin: Jokaisen hyvän pelaajan kädet on liikkeessä ylläviistoon jo pitkän matkaa ennen osumaa. Silti lapa voi olla laskussa tai nousussa, vahventua tai heikentyä, aueta tai sulkeutua osuma-alueella.
Ratkaise nyt tuo yhtälö ensin itsellesi ja mieti sitten mihin muuhun laskelmissasi se voi vaikuttaa.

Samaan aikaan lavalla on reilusti enemmän nopeutta kuin käsillä, mutta kehällä se ei saavuta niitä vielä pitkään aikaan, puhumattakaan että ohittaisi ne. Lisäksi niillä on täysin eri kulkusuunta myös kohteeseen nähden.

Eli ihan huoletta saat työntää nuo laskelmasi johonkin pimeään paikkaan, koska niistä puuttuu lähes täyden vapausasteen nivel ranteiden kohdalta, sekä myös varsin suuren vapausasteen muita niveliä tuolta sisempää ja ylempää järjestelmästä. Se ei todellakaan ole around the fixed hub vaan kaukana siitä.

[PG]

Jake2 kirjoitti: (30.4.2011 17:07:16)

PG kirjoitti: (30.4.2011 15:50:35)
Jake, luulen että ainakin sinä pystyt palauttamaan mieleesi avaruusgeometria opit. Luulen myös, että pyrit etsimään totuutta asiassa. Siksi olisi kiva, jos perehtyisit tosissasi laskelmani perusteisiin ja tekisit itse johtopäätökset.

Tällä hetkellä tuntuu olevan tärkeämpääkin tekemistä kuin johtaa kaavoja ja katsoa tuleeko samat tulokset. Oletan että laskelmat ovat oikein. Toisaalta kun kaksi tahoa toisistaan riipumatta väittää mitanneensa kameratekniikalla mailan lavan suoria liikeratoja, mietin mm. voisiko laskelmien olettamuksissa olla jotain mikä poikkeaa todellisuudesta. Toinen vaihtoehtohan on että mittausmenetelmissä tai tulosten tulkinnassa on jotain epätarkkuuksia.

OK. Ymmärrän hyvin. Tärkeämpää tekemistä kuin perustella päivän selviä asioita olisi minullakin. Hyvä, että et lähtenyt johtelemaan, janojen keskipisteiden koordinaatteihin lipsahti vappukiireessä virheitä. (Oikeat koordinaatit ovat AB:lle (a/2,b,0) ja CD:lle (x/2,y/2,(z+c)/2). Tämä niille, joilla olisi aikaa ja mielenkiintoa.)

En ole viimeaikoina ehtinyt tarkkaan lukemaan kaikkia viestejä. Mitkä ovat nämä kaksi tahoa, jotka väittävät mitanneensa kameratekniikalla mailan lavan suoria liikeratoja? Virhelähteitä luulisi olevan paljon ja laskentaakin tarvitaan, vaikka laitteet itse sen hoitaisivat. Esittämäni kirjainyhtälöt perustuvat 2500 vuotta vanhaan tietoon (Pythagoraan väittämä kuusi kertaa, ei muuta). Sitä tietoa ei ole kumottu. Oletuksena taipumaton varsi, sweet spot kulkee suoraa rataa pisteestä A pisteeseen B tietyn matkan ja grippipää samanaikaisesti pisteestä C pisteeseen D tietyn matkan. Pisteiden A, B ja C koordinaatit tunnetaan, mitkä ovat pisteen D koordinaatit? Puhdas matemaattinen tehtävä, jolla ei ole erilaisten svingitekniikoiden kanssa mitään tekemistä.

[PG]

ts kirjoitti: (30.4.2011 16:37:58)

PG kirjoitti: (30.4.2011 15:50:35)

AC = grippipään etäisyys mailanpäästä = L. Se on suorakulmaisen kolmion OAC hypotenuusa. Sen kateetit ovat OC = c ja äsken laskettu OA. Pythagoraan lauseella saadaan L = (OA²+ OC²)^( ½ ) eli L = (a²+b²+c²)^(1/2), josta c = (L² – a² – b²)^( ½ ), eikö vain?

.

Tuossa kohdassa menet metsään golflyönnin tarkastelun kannalta ja siksi romuttuu koko ajattelusi siitä. Tarkastelet sitä edelleen kehänopeuksien kautta etkä kohteen tai pallon lähtösuunnan suhteen.

Molemmat täytyy ymmärtää, mutta lavan reitin kannalta kehänopeuksien ja heilurimallin kautta kähestyminen johtaa vain syvälle suohon.

Pystyäkseen pelaamaan tuloksellista golfia, pitää pelaajan minimoida lavan rotaatio ja sen kulkeman radan kaaren jyrkkyys, silti riittävä nopeus ylläpitäen. Mitä pidemmän suoran osuuden pelaaja oppii noilla reunaehdoilla tuottamaan suhteessa haluttuun lähtösuuntaan, sen paremmin hän tehtävistään kentällä selviytyy niinäkin päivinä, kun hermotus ei ole herkimmillään.

Sen sijaan, että pyörit laskelmissasi tuon heilurimallin parissa, ottaisit tarkasteluun mittaustulokset, joissa selkeästi todetaan lavan liikkuvan suoraan haluttuun suuntaan osuma-alueella ja mietisit mikä tuon mahdollistaa. Sitä kautta ymmärtäisit myös sen, miksi suoraan ja suorassa kulkevan lavan kannalla ja kärjellä on sama nopeus.

Outoja kirjoittelet (mm. heilurimalli). Outoja väität (mm. suorassa kulkevan lavan kannalla ja kärjellä on sama nopeus). Kaari on kaari ja se näkyy kaarena myös kaikissa projektioissa paitsi kaaren tasoa vastaan kohtisuorissa olevissa projektioissa. Niistä tuskin on kysymys. Sitä paitsi et puhu mistään projektiosta, vaan esim., että ’selkeästi todetaan lavan liikkuvan suoraan haluttuun suuntaan’.

Noista mainitsemistasi mittaustuloksista olen kiinnostunut.

[PG]

ts kirjoitti: (29.4.2011 23:07:50)

PG kirjoitti: (29.4.2011 22:27:26)

Hyvällä syyllä voidaan kysyä: Mihin suuntaa pitää kiskaista, jotta sekä mailanpää, että gippipää kulkevat suoraan? Jos ratkaisu on olemassa, niin se voidaan selvittää vain matematiikan avulla.

Mulla on sulle tehtävä. Tunget sen laskukoneen ja excelin nyt sivuun ja otat mailan käteen. Menet seinän viereen niin, että lavan kärki on kiinni seinässä ja otat alkuasennon. Kokeile saatko tehtyä liikkeen niin että lavan kärki osuman seudulla pysyy noin 20cm matkan kiinni seinässä. Itse pystyin pitämään noin 40cm, mutta 20 on hyvä alku.

Sitten kun ymmärrät miten tuo tapahtuu, voita palata työpöydän ääreen ihmettelemään tapahtunutta. Jos et saa, opettele lyömään sitä golfpalloa oikein.

Juu, tein niin. Lavan kärki pysyi kaksi metriä seinässä kiinni, mutta kädet liikkuivat puolitoista metriä ja svingi oli aika omituinen. Ei vakuuttanut.

Sen sijaan kun otin teräsmittanauhan ja liikutin sen toista päätä 20 cm pöydän suoraa reunaa pitkin ja toista päätä samanaikaisesti 3 cm, tulin vakuuttuneeksi siitä, mitä puhdas matematiikkakin jo kertoo. Kaamea käppyrä, jonka tekeminen puolessa sadasosasekunnissa ei onnistu keneltäkään. Grippipään liikuttaminen sopivaan suuntaan ja eri tasossa missä mailanpää liikkuu loiventaa käppyrän kaarevuutta, mutta ei poista sitä.

[PG]

ts kirjoitti: (29.4.2011 23:00:38)

PG kirjoitti: (29.4.2011 19:51:44)
Oli kiire reissulta kotiin. Auton renkaiden kulutuspintojen nopeus oli parhaimmillaan 240 km/h, kulmanopeus hurja 6400 deg/s. Poliisi valvoi liikennettä. Ei pysäyttänyt. Miksi? Oli se villiä menoa. Pyörimisen keskipiste ei pysynyt hetkeäkään paikallaan. .

On varmaan villiä, kun on ensin laskelmillaan osoittanut renkaan ulko- ja sisäreunan pyörivän suoraan ajetaessakin eri nopeudella.

Näinhän se on, paitsi silloin, kun tarkastellaan niitä ulko- ja sisärenkaan pisteitä, jotka ovat samalla korkeudella maasta. Hyvä ts, alat vähitellen oppia…

[ts]

TeeUrpo kirjoitti: (30.4.2011 17:38:53)
Jake2 onnittelut viesti no 900.

Jake2, PG ja ts.

Katsokaapa tätä linkkiä, saattaa muuttaa ajatuksia.

All wrong

Ei varmasti muuta AJ:n ajatukset omiani. Tuossa suossa on rämmitty ihan tarpeeksi kauan.

[TeeTurbo]

Jake2 onnittelut viesti no 900.

Jake2, PG ja ts.

Katsokaapa tätä linkkiä, saattaa muuttaa ajatuksia.

All wrong

[Jake2]

PG kirjoitti: (30.4.2011 15:50:35)
Jake, luulen että ainakin sinä pystyt palauttamaan mieleesi avaruusgeometria opit. Luulen myös, että pyrit etsimään totuutta asiassa. Siksi olisi kiva, jos perehtyisit tosissasi laskelmani perusteisiin ja tekisit itse johtopäätökset.

Tällä hetkellä tuntuu olevan tärkeämpääkin tekemistä kuin johtaa kaavoja ja katsoa tuleeko samat tulokset. Oletan että laskelmat ovat oikein. Toisaalta kun kaksi tahoa toisistaan riipumatta väittää mitanneensa kameratekniikalla mailan lavan suoria liikeratoja, mietin mm. voisiko laskelmien olettamuksissa olla jotain mikä poikkeaa todellisuudesta. Toinen vaihtoehtohan on että mittausmenetelmissä tai tulosten tulkinnassa on jotain epätarkkuuksia.

[ts]

PG kirjoitti: (30.4.2011 15:50:35)

AC = grippipään etäisyys mailanpäästä = L. Se on suorakulmaisen kolmion OAC hypotenuusa. Sen kateetit ovat OC = c ja äsken laskettu OA. Pythagoraan lauseella saadaan L = (OA²+ OC²)^( ½ ) eli L = (a²+b²+c²), josta c = (L² – a² – b²)^( ½ ), eikö vain?

.

Tuossa kohdassa menet metsään golflyönnin tarkastelun kannalta ja siksi romuttuu koko ajattelusi siitä. Tarkastelet sitä edelleen kehänopeuksien kautta etkä kohteen tai pallon lähtösuunnan suhteen.

Molemmat täytyy ymmärtää, mutta lavan reitin kannalta kehänopeuksien ja heilurimallin kautta kähestyminen johtaa vain syvälle suohon.

Pystyäkseen pelaamaan tuloksellista golfia, pitää pelaajan minimoida lavan rotaatio ja sen kulkeman radan kaaren jyrkkyys, silti riittävä nopeus ylläpitäen. Mitä pidemmän suoran osuuden pelaaja oppii noilla reunaehdoilla tuottamaan suhteessa haluttuun lähtösuuntaan, sen paremmin hän tehtävistään kentällä selviytyy niinäkin päivinä, kun hermotus ei ole herkimmillään.

Sen sijaan, että pyörit laskelmissasi tuon heilurimallin parissa, ottaisit tarkasteluun mittaustulokset, joissa selkeästi todetaan lavan liikkuvan suoraan haluttuun suuntaan osuma-alueella ja mietisit mikä tuon mahdollistaa. Sitä kautta ymmärtäisit myös sen, miksi suoraan ja suorassa kulkevan lavan kannalla ja kärjellä on sama nopeus.

[TeeTurbo]

PG kirjoitti: (30.4.2011 15:50:35)
Jake, luulen että ainakin sinä pystyt palauttamaan mieleesi avaruusgeometria opit. Luulen myös, että pyrit etsimään totuutta asiassa. Siksi olisi kiva, jos perehtyisit tosissasi laskelmani perusteisiin ja tekisit itse johtopäätökset. Asiaan sisälle pääsyn helpottamiseksi : Piirrä x,y,z- koordinaatisto tavalliseen tapaan z- akseli pystysuoraan, y- akseli vaakasuoraan ja x- akseli 135 asteen kulmassa edellisiin nähden. (Todellisuudessa x- akseli on kohtisuorassa piirustustasoa vastaan). Merkitse xy- tasoon piste A(a,b,0), y-akselille piste B pisteeseen (0,b,0) ja z- akselille C kohtaan (0,0,c). Merkitse piste D(x,y,z) jonnekin sinne C:n lähimaastoon. Skaalalla ei niin ole väliä, piirros on periaatteellinen. Yhdistä pisteet A ja B, A ja C, B ja C, B ja D sekä C ja D.

Pisteen A etäisyys origosta =OA saadaan Pythagoraan lauseen avulla kolmiosta, jonka kateetit ovat a ja b.

AC = grippipään etäisyys mailanpäästä = L. Se on suorakulmaisen kolmion OAC hypotenuusa. Sen kateetit ovat OC = c ja äsken laskettu OA. Pythagoraan lauseella saadaan L = (OA²+ OC²)^( ½ ) eli L = (a²+b²+c²), josta c = (L² – a² – b²)^( ½ ), eikö vain?

Lopputilanteessa mailanpää on pisteessä B(0,b,0) ja grippipää pisteessä D(x,y,z). Vektorin pituus on tunnetusti ((x-x1) ²+(y-y1) ²+(z-z1)²)^( ½ ). Tässä siis BD = L = ((x-0)²+(y-b)²+(z-0 ²)^( ½ ) eli pelkistettynä

L = (x²+(y-b)²+z²)^( ½ )

Vektorin CD alkupiste C on (0,0,c) ja loppupiste D(x,y,z). Näin ollen vektorin CD pituus k = ((x-0)²+(y-c)²+(z-0)²( ½ ) eli

k = (x²+y²+(z-c)²)( ½ )

Korottamalla yhtälöiden molemmat puolet toiseen, saadaan

L² = x²+(y-b)²+z² … (1)
k² = x²+y²+(z-c)²… (2)

Pelkkää Pythagoraan lauseen soveltamista. Pysyit varmaan kärryillä. Muistin virkistämiseksi (a-b)² = a²- 2ab +b². Sovella myös sitä, vähennä yhtälöt (1) ja (2) puolittain toisistaan ja saata johto loppuun asti. Uskon, että päädyt samaan tulokseen, johon itsekin päädyin. Tai sitten olet unohtanut perusmatematiikan täydellisesti :(.

Siihen käyryystarkasteluun tarvitset vielä janojen AB ja CD keskipisteiden koordinaatit. Ne ovat AB:lle (a/2,b/2,0) ja CD:lle (x/2,y/2,(z-c)/2). Ei niitä mailanpään ja käsien mahdolliset kiihtyvyydet tai hidastuvuudet paljon hetkauta, koska vaikutusaika on vain alle puoli sadasosasekuntia.

Meillä mökkikentällä tuolla keskisessä Suomessa eräs matemaatikko aloitti golfin peluun. Kun sattui samaan aikaan kierrokselle tämän kävelevän tiestsikan kanssa, saattoi olla varma, jotta etuysi kesti kolmisen tuntia, kun kaveri laskeskeli ja mittaili lyöntiensä kaaria ja puttien linjoja. Hidas peli tuli siitä, että laskelmat olivat päin prinkkalaa. Nykyään samainen velho on oiva golfari ja myöntää, että harjoittelu ja oppiminen ovat avain golfiin, eikä siitä teoriasta paljon kannata välittää, kun tuppaa rundit menemään hitaaksi.

PS. Kukakohan saa kirjoittaa viestin no 1000 ?

[PG]

Jake, luulen että ainakin sinä pystyt palauttamaan mieleesi avaruusgeometria opit. Luulen myös, että pyrit etsimään totuutta asiassa. Siksi olisi kiva, jos perehtyisit tosissasi laskelmani perusteisiin ja tekisit itse johtopäätökset. Asiaan sisälle pääsyn helpottamiseksi : Piirrä x,y,z- koordinaatisto tavalliseen tapaan z- akseli pystysuoraan, y- akseli vaakasuoraan ja x- akseli 135 asteen kulmassa edellisiin nähden. (Todellisuudessa x- akseli on kohtisuorassa piirustustasoa vastaan). Merkitse xy- tasoon piste A(a,b,0), y-akselille piste B pisteeseen (0,b,0) ja z- akselille C kohtaan (0,0,c). Merkitse piste D(x,y,z) jonnekin sinne C:n lähimaastoon. Skaalalla ei niin ole väliä, piirros on periaatteellinen. Yhdistä pisteet A ja B, A ja C, B ja C, B ja D sekä C ja D.

Pisteen A etäisyys origosta =OA saadaan Pythagoraan lauseen avulla kolmiosta, jonka kateetit ovat a ja b.

AC = grippipään etäisyys mailanpäästä = L. Se on suorakulmaisen kolmion OAC hypotenuusa. Sen kateetit ovat OC = c ja äsken laskettu OA. Pythagoraan lauseella saadaan L = (OA²+ OC²)^( ½ ) eli L = (a²+b²+c²), josta c = (L² – a² – b²)^( ½ ), eikö vain?

Lopputilanteessa mailanpää on pisteessä B(0,b,0) ja grippipää pisteessä D(x,y,z). Vektorin pituus on tunnetusti ((x-x1) ²+(y-y1) ²+(z-z1)²)^( ½ ). Tässä siis BD = L = ((x-0)²+(y-b)²+(z-0 ²)^( ½ ) eli pelkistettynä

L = (x²+(y-b)²+z²)^( ½ )

Vektorin CD alkupiste C on (0,0,c) ja loppupiste D(x,y,z). Näin ollen vektorin CD pituus k = ((x-0)²+(y-c)²+(z-0)²( ½ ) eli

k = (x²+y²+(z-c)²)( ½ )

Korottamalla yhtälöiden molemmat puolet toiseen, saadaan

L² = x²+(y-b)²+z² … (1)
k² = x²+y²+(z-c)²… (2)

Pelkkää Pythagoraan lauseen soveltamista. Pysyit varmaan kärryillä. Muistin virkistämiseksi (a-b)² = a²- 2ab +b². Sovella myös sitä, vähennä yhtälöt (1) ja (2) puolittain toisistaan ja saata johto loppuun asti. Uskon, että päädyt samaan tulokseen, johon itsekin päädyin. Tai sitten olet unohtanut perusmatematiikan täydellisesti :(.

Siihen käyryystarkasteluun tarvitset vielä janojen AB ja CD keskipisteiden koordinaatit. Ne ovat AB:lle (a/2,b/2,0) ja CD:lle (x/2,y/2,(z-c)/2). Ei niitä mailanpään ja käsien mahdolliset kiihtyvyydet tai hidastuvuudet paljon hetkauta, koska vaikutusaika on vain alle puoli sadasosasekuntia.

[PG]

Jake2 kirjoitti: (30.4.2011 0:25:18)
Tarkastelu osumassa ja sen jälkeen onkin kai vaikeampaa kun lapa hidastuu ja kuvittelisin osumavoimalla olevan alaspäin painavaa komponenttia.

Osumavoiman mahdollinen alaspäin painava komponentti ei vaikuta mitään laskelmassani, siinähän oletetaan että mailanpää kulkee suoraa rataa myöten ennen osumaa ja osuman jälkeen. Tosin osuman jälkeen mailanpään ja myös käsien nopeus putoaa, se jonkin verran vaikuttaa. Mutta miksi mailanpään pitäisi kulkea suoraan vielä osuman jälkeenkin.

Noissa Brianin piirroksissa oli se pieni vika, että mailanpää porhalsi entistä vauhtia osuman jälkeenkin. Lisäksi tarkastelu tapahtui tasossa. Piirroksista havaitaan, että grippipään nopeuden suunta poikkeaa erittäin jyrkästi mailanpään nopeuden suunnasta silloin, kun mailanpää menee suoran. Näin siinä todellakin käy, mikäli mailanpää ja grippipää kulkevat samassa tasossa. Grippipää ei tietenkään voi mennä suoraa rataa.

[PG]

Jake2 kirjoitti: (30.4.2011 14:40:55)

PG kirjoitti: (30.4.2011 11:39:09)
Aiheellinen kysymys. Jotta ei tarvitsisi hirveästi spekuloida, niin olisi hyvä tietää, missä rajoissa mailanpään ja käsien nopeudet yleensä muuttuvat eli mitkä ovat kiihtyvyydet ja hidastuvuudet juuri ennen osumaa noin 0,005 s aikana (vastaa kutakuinkin yhtä frameväliä 170 fps- graafissa). Pelimiehen 4D-graafin perusteella käsien nopeus pysyy juuri ennen osumaa vakiona, mutta mailanpää kiihtyy osumaan asti 277 m/s^2. Sen mukaan mailanpää liikkuisi 20 cm sijaan 20,3 cm (eli kaavassa a = 20,3 cm) ja kädet liikkuisivat omaan suuntaansa – mikä lie – edelleen sen 3 cm. Tässä tapauksessa käsi- ja lapanopeuden muutoksilla 0,0046 s ( = 20 cm/97,8 mph) aikana ei ole mitään merkitystä, olkoon L:n arvo mikä hyvänsä.

Meinasin vaan että tuosta johtuen geometrisen laskelmasi janojen keskipisteiden välinen etäisyys ei ole ajaliisesti oikein, mutta muuttaako tulosta merkiitvästi?
Toinen mikä tulee mieleen on siten tuo varren kiertyminen joka siirtää lapaa suhteessa grippiin, paljonko se voi vaikuttaa?

Janan keskipiste muuttuu todella vähän, mikäli tasaiset vaudit muuttuvat kiihtyvyyksiksi tai hidastuvuuksiksi. Tässä tapauksessa janan AB keskipisteen x- koordinaatti muuttuisi 10 cm -> 10,15 cm, muut koordinaatit samoja. Käsinopeus pysyy samana => keskipisteen koordinaatit samoja. Ei tällä asialla ole käytännön merkitystä.

Tuo varren kietyminen liittyy paremminkin lavan eri pisteiden väliseen nopeustarkasteluun. Lähtökohtana tässä on se, että lavan suoraan meneminen on sama kuin sweet spotin suoraan meneminen ja että grippipää on täsmällisesti määrätty gripin piste, jonka sijaintia ei varren kietyminen muuta.

[Jake2]

PG kirjoitti: (30.4.2011 11:39:09)
Aiheellinen kysymys. Jotta ei tarvitsisi hirveästi spekuloida, niin olisi hyvä tietää, missä rajoissa mailanpään ja käsien nopeudet yleensä muuttuvat eli mitkä ovat kiihtyvyydet ja hidastuvuudet juuri ennen osumaa noin 0,005 s aikana (vastaa kutakuinkin yhtä frameväliä 170 fps- graafissa). Pelimiehen 4D-graafin perusteella käsien nopeus pysyy juuri ennen osumaa vakiona, mutta mailanpää kiihtyy osumaan asti 277 m/s^2. Sen mukaan mailanpää liikkuisi 20 cm sijaan 20,3 cm (eli kaavassa a = 20,3 cm) ja kädet liikkuisivat omaan suuntaansa – mikä lie – edelleen sen 3 cm. Tässä tapauksessa käsi- ja lapanopeuden muutoksilla 0,0046 s ( = 20 cm/97,8 mph) aikana ei ole mitään merkitystä, olkoon L:n arvo mikä hyvänsä.

Meinasin vaan että tuosta johtuen geometrisen laskelmasi janojen keskipisteiden välinen etäisyys ei ole ajaliisesti oikein, mutta muuttaako tulosta merkiitvästi?
Toinen mikä tulee mieleen on siten tuo varren kiertyminen joka siirtää lapaa suhteessa grippiin, paljonko se voi vaikuttaa?