Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros
-
JulkaisijaArtikkelit
-
Liikaa, kun linttaantuu, niin sitä enemmän woblaileepi alkumatkalla ja aiheuttaa aerodynaamisesti kovin vähän toivottuja muotoja tälläinen eri-pehmeä pallo, johon aiemmin viitattiin.
Kontaktiaika kyllä pitenee, mutta kustannuksella.
PG
Huomasitko tätä:Huomasin. Siinähän se Tutelman just oikaisee ja ajattelee tilanteen vähän väärin. Kirjoittelin tuossa edellä tämän:
Otetaas tähän pari esimerkkiä.
1. Pallon ja lavan välissä on vieteri, kaikki on paikallaan. Lapaa työnnetään voimalla X sen aikaa kun vieteri puristuu ja sitten vapautuu. Kitkaa ei ole. Onko pallolla ja lavalla sama vauhti kun vieteri on purkautunut? Ei ole, pallolla on kovempi vauhti.
2. Sama mutta ilman vieteriä. Sama voima ja sama kesto. Pallo ja lapa liikkuvat yhtä matkaa joten nyt niillä on sama vauhti lopussa.
Tutelman laskee tilanteen tuolla tavalla 2. Todellisuudessa siinä on kuitenkin tuo jousi välissä [golf-pallon puristuminen osumassa], joten lopputuloskin on eri.
Se ’pitkä flippaus’ on hyvä esimerkki tuosta vaihtoehdosta 2. Ja, jos miettii mikä on tilanne tässä vaihtoehdossa esim sekunti tuon jälkeen, niin pallo ja lapa jatkavat matkaansa edelleen yhdessä, ja samalla vauhdilla (olettaen että lapa ei ole mailassa kiinni vaan on irtonainen).
Vaihtoehdossa 1 sen sijaan tuo vieteri/jousi työntää palloa ja lapaa erilleen toisistaan, ja sen seurauksena ne saa eri vauhdin. Niiden yhteinen massakeskipiste saa tuon ’saman vauhdin’ (liikemäärät ja energiat täytyy säilyä), mutta ei niillä keskenään sama vauhti ole. Esim, sekuntia myöhemmin pallo on jo mennyt menojaan koska sillä on kovempi vauhti. Pallon ja lavan eri massa (pallo on paljon kevyempi) vaan korostaa tuota vauhdin eroa.
Golf-lyönti on vaihtoehdon 1 mukainen tapahtuma, oli siinä mukana tukivoimaa tai sitten ei. Pallo puristuu kasaan ja palautuu, ja se on erittäin tiukka/voimakas jousi samalla. Kaikki tää tapahtuu erittäin lyhyen ajan sisällä. Lapa ehtii liikkua osuman aikana n. puolitoista senttiä eteenpäin, ja sinä aikana tuo tapahtuu.
Kuva kertoo enemmän kuin tuhat sanaa.
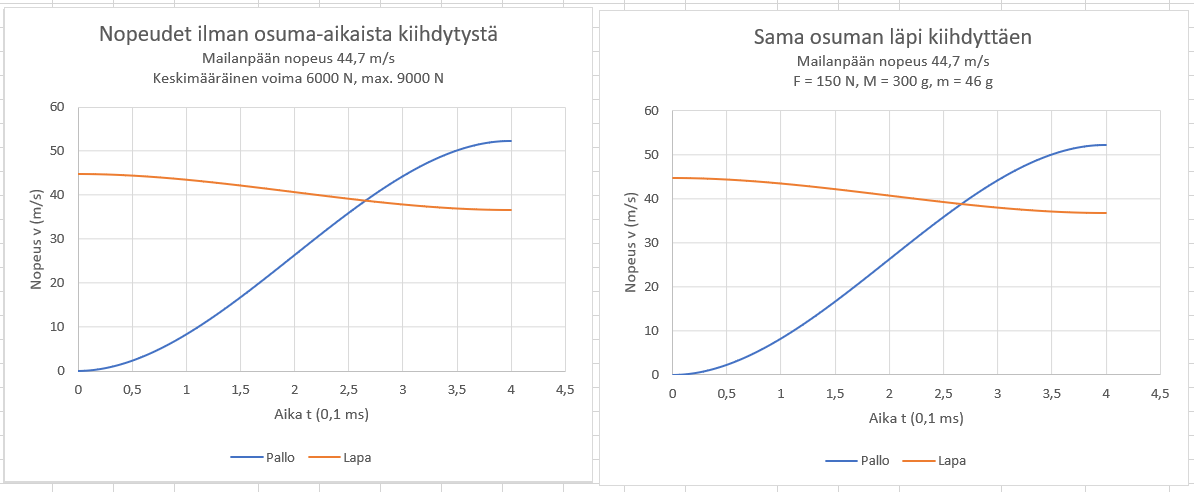
Tukivoima siis johtaa siihen että lavan ja pallon vauhti on aina sama osuman lopussa, ja lapa menee pallosta ohi heti osuman jälkeen? Käppyröiden jatkuminen toisi sen hyvin esiin, mutta näkeehän sen jo noista kuvista. Onkohan meillä kysymyksenasettelussa joku vika että näin käy? Lisäksi, kaikki hyvät pallonlyöjät ovat väärässä vaikka osaavat palloa lyödä hyvin.
Taidan vetäytyä tauolle tästä keskustelusta.Lineaarisessa liikkeessä, kun mailanpäähän kohdistuu vakiovoima, mailanpää kiihtyy jatkuvasti eli nopeus kasvaa lineaarisesti ajassa. Kun pallo tulee ”kyytiin”, kiiihtyvyys laskee, koska kokonaissysteemin massa kasvaa, mutta mailanpään nopeus on edelleen kasvava.
Oletetaanpa, että pallo irtoaisi mailan lavasta. Tällöin palloon ei kohdistu voimia, joten sen nopeus on vakio ja lineaarisessa liikkeessä mailan pää kasvavalla nopeudellaan saa pallon uudestaan kiinni. Eli jos tuota aika-nopeus -käyräparia jatketaan, tosiaan maila menee pallon ”ohi”, toisin sanoen puristaa palloa (=jousi) kasaan uudelleen (= kaksoiskosketus). Lopputuloksena siis käyräpari, jossa mailanpään nopeus kasvaa noin (kaksi eri kulmakerrointa, jos pallo välillä irtoaa mailasta) lineaarisesti maailman tappiin ja pallon nopeuskäyrä oskilloi mailanpään käyrän ympärillä (=moninkertainen kosketus). Jos pallo käsitetään pelkäksi jouseksi (ei energiahäviötä), oskilloinnin amplitudi pysyy vakiona. Käytännössä pallossa on häviöitä, jolloin mailan pää ja pallo päätyvät lopulta matkustamaan yhdessä samalla nopeudella (=flippaus).
Miksi sitten pallo ja mailan pää todellisuudessa eroavat toisistaan – onhan läsnä aina jokin, ainakin pieni tukivoima? Mailan pää ei ole lineaarisessa liikeessä vaan ympyräliikkeessä kun taas pallo saa suunnilleen (kierre unohtaen) lineaarisen liikemäärän. Käytännössä lienee niin, että pallo irtoaa lavasta ja ennen kuin lapa saa sen uudelleen kiinni, liikeradat ovat eronneet siksi paljon, että tuota toista kohtaamista ei tule.
Tämän itsestäänselvyyden puinnin sijaan mielenkiintoisempaa olisi miettiä pallon lineaarisen ja pyörimisnopeuden syntyä, joka on seurausta siitä, että mailanpään massakeskipisteen liikerata ei kulje pallon massakeskipisteen suuntaan vaan palloon kohdistuu sekä radiaalinen että tangentiaalinen komponentti.
Tukivoima siis johtaa siihen että lavan ja pallon vauhti on aina sama osuman lopussa,
Tuossa osatarkastelussa kyllä. Vieläpä riippumatta siitä, kuinka paljon pallo puristuu tukivoiman vaikutuksesta kokoon. Miten se muutenkaan voisi olla? Lähteväthän lapa ja pallo kumpikin levosta liikkeelle. Lapa puskee palloa koko kontaktin ajan eteenpäin keskimäärin 20 N voimalla. Tästä lavan puskemisesta ja voimasta pallo vauhtinsa saa. Ei tätä yhteiseloa kuitenkaan kauan kestä. Se 6000 N voima pitää huolen siitä, että kontakti on kovin lyhyt. Kontaktin loppupuolella palloon kohdistuva voima väistämättä hupenee mennen lopuksi nollaan, samalla kun lapa saa takaisin sen voiman ja kiihtyvyyden, joka sillä liikkeellelähdön alussa oli.
Varsinaisessa golflyönnissä lapa törmää kovalla vauhdilla palloon. Siinä käy sitten niin kuin ne kaksi viimeistä graafia osoittavat, toinen ilman tukivoimaa,toinen sen kera. Jo kontaktin aikana pallon massakeskipiste ylittää lavan nopeuden, mutta kokoonpuristuma on vielä siinä vaiheessa suuri. Kontakti päättyy, kun pallon muoto on palutunut. Irtautuessaan lavasta pallon massakeskipisteen vauhti on huomattavasti lavan vauhtia suurempi.
Muuten, kuinka paljon pallo puristuu kokoon 20 N voiman vaikutuksesta? Riippuu tietenkin pallon kovuudesta. Jos 6000 N:lla puristuu 10 mm, niin 20 N:lla se voisi olla 0,03 mm luokkaa.
Lisäksi, kaikki hyvät pallonlyöjät ovat väärässä vaikka osaavat palloa lyödä hyvin.
Miten tuo liittyy tähän asiaan?
[Ja energiat ja liikemäärät pitää toki säilyä, en ole fysiikan lakeja tässä muuttamassa]
Jos tukivoiman osuma-aikana tuottama liikemäärä jaetaan tasan lavan ja pallon kesken, niin liikemäärät säilyvät, mutta energiat eivät. Jos M=300g ja m=46g, energiamäärä kasvaa yli kaksinkertaiseksi todellisuuteen verrattuna. (Yleisesti ottaen (M+m)^2/(4M*m) -kertaiseksi)
Ja ikiliikkuja on syntynyt…
Vaihdoin draiveriin.
Ihme keskustelu, tää ei jätä rauhaan. Joku on varmaan väärässä internetissä…
PG – älä lyö lyötyä, mielestäni olin jo sanonu että toi mun lasku oli väärin, joten ei tarvi toistaa.
PappaTykki – ymmärsin kyllä oskilloinnin merkityksen ja että lapa jatkaa kiihtymistään. Mutta tuntui vaan erikoiselta (ja vaikka PG:n kuvat on hienot) että samaan aikaan kun on menossa todella kova törmäys ja lapa hidastuu isosti, niin samalla flippaillaan vihellellen ja lapa (kuvaannollisesti) ohittaa siinä sitten pallon.
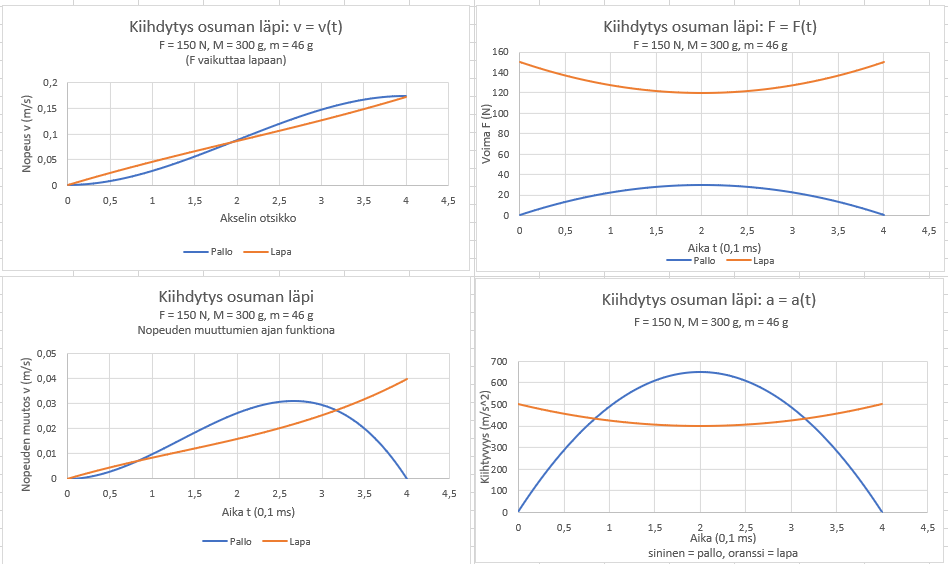
Sitten eteenpäin. Muutama asia jossa mua ei ole vielä lakaistu maton alle taitaa sisältää seuraavat: 1) pallo puristuu osuman aikana ja siinä on isot voimat ja jousivoima mukana, 2) jousivoima työntää lapaa ja palloa poispäin toisistaan, 3) jousivoiman vaikutuksesta kevyempi (pallo) saa isomman vauhdin [vauhdin muutoksen] kuin paivanampi (lapa). Kohdat 2 ja 3 on normaalia fysiikkaa ja kohta 1 on nähty kuvista ja hidastusvideoista.
No, mietinpä seuraavaa. Varmaan 90% osuman ajasta pallon puristuksen jousivoima on isompi kuin se esimerkkinä käytetty 150N tukivoima. Alun ja lopun 5% ajasta tukivoima varmaan kohdistuu niin kuin PG on kuvannut (vähäisessä määrässä jo jousivoima vastaan), mutta lopun ajasta se toimii eniten tuota pallon jousivoimaa vastaan (voima ja vastavoima). Se tekee siis työtä jousta vastaan, kerryttää potentiaalienergiaa ja joka sitten purkautuu. Tuo puolestaan sitten työntää palloa ja lapaa eri suuntiin (vastakkaisiin suuntiin), ja tässä tilanteessa pallo saa näistä kahdesta isomman vauhdin / vauhdin muutoksen. Näin siis tuo tukivoima ei pelkästään kiihdytä lavan ja pallon yhteistä massaa vaan painii tuota jousivoimaa vastaan. Ja, se ei olekaan lavan kiihdytys joka vaikuttaa pallon nopeuteen vaan toi jousivoima, ja tukivoiman vaikutus siihen.
Noi prosentit on hatusta, mutta itse ajatus on mielenkiintoinen. Noinhan siinä suurin piirtein tapahtuu. Miten se vaikuttaa laskentaan, joku muu saa arvioida ja luultavasti taas kerran tyrmätä.
NimetönIhme keskustelu, tää ei jätä rauhaan. Joku on varmaan väärässä internetissä…
Klassikko!

Swinger, viestin 1) 7.4.2021 13:15:27 ylin graafi vasemmalla ja viestin 2) 7.4.2021 17:20:55 vasen graafi tulee tulkita yhdessä.
1) kertoo, että tukivoiman tuottama nopeus pallolle ja lavalle on kontaktin lopussa n. 0,2 m/s.
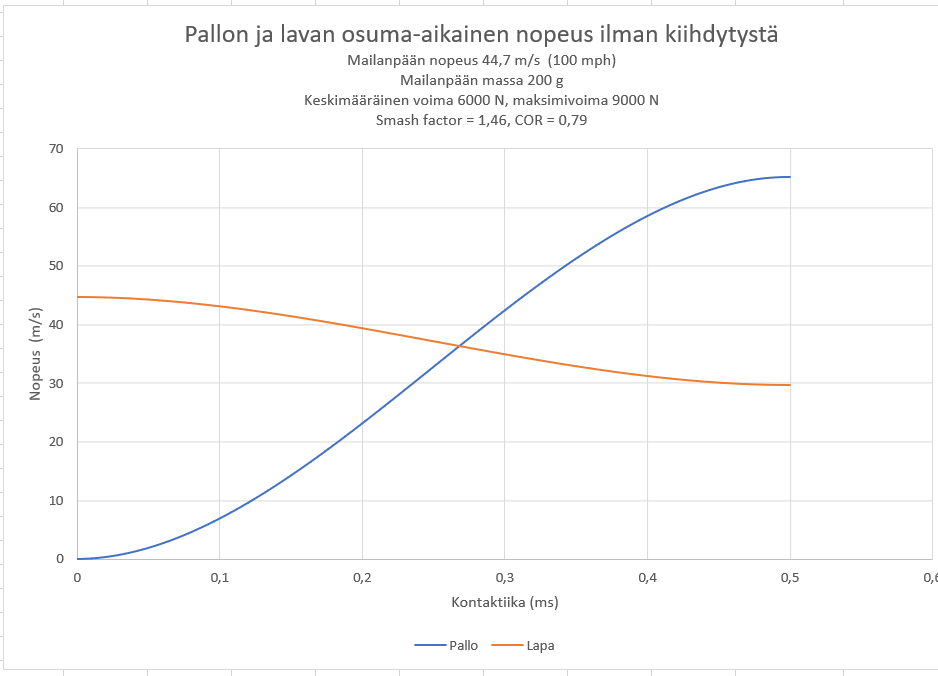
2) kertoo, että törmäyksen tuottama nopeus kontaktin lopussa on pallolle n. 52 m/s ja lavalle n. 37 m/s.
Kun ne yhdistetään, saadaan graafi 3) 7.4.2021 17:20:55 oikealla = lyönnin lopputulos.
Lapa ei siis voi mennä pallon ohi, koska kontaktin lopussa pallolla on paljon suurempi nopeus kuin lavalla.
Huom! Ojalan laskuoppi sanoo: 1 + 2 = 3. Newtonin Philosophiae Naturalis Principia Mathematica sanoo: 1) + 2) = 3)
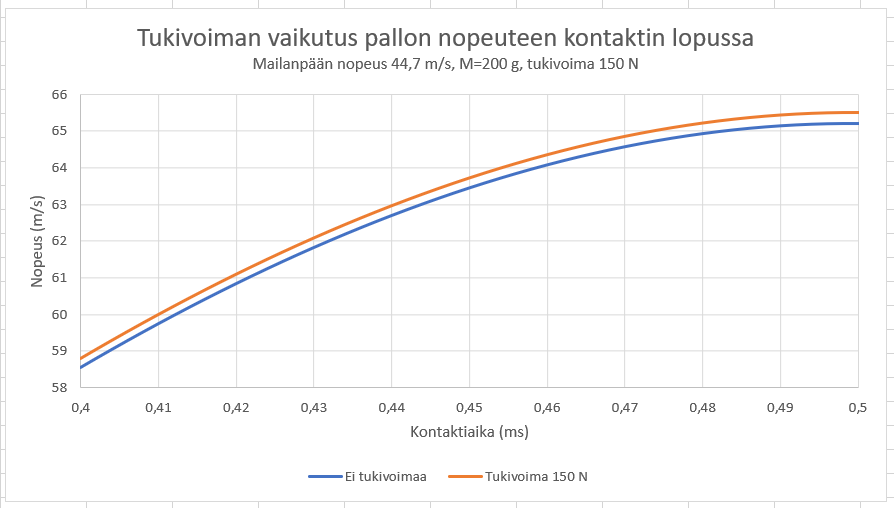
Tässä vielä uusi graafi ihmeteltäväksi.

Ja joku vielä sanoo, ettei tukivoimalla muka ole merkitystä pallon lähtönopeuteen!
Swinger: Näin siis tuo tukivoima ei pelkästään kiihdytä lavan ja pallon yhteistä massaa vaan painii tuota jousivoimaa vastaan. Ja, se ei olekaan lavan kiihdytys joka vaikuttaa pallon nopeuteen vaan toi jousivoima, ja tukivoiman vaikutus siihen.
Tarkoitatko, että osumassa vaikuttaa tukivoiman (F1) lisäksi jousivoima (F2), jolloin kokonaisvoima F = F1+F2? Ja tämä voima (F) vaikuttaa jollakin tavalla lavan ja pallon nopeuteen, jonka seurauksena pallo saa suuremman nopeuden ja vastaavasti lapa saa pienemmän nopeuden, kuin olen laskenut? (Esimerkeissämme tukivoima F1 on ollut 150 N. Käytetään sitä jatkossakin, mikäli jatkolaskenta on tarpeen. Jousivoiman F2 suuruutta ei tarvitse toistaiseksi tietää).
Vai tarkoitatko, että kaava F = ma ei päde, jos kappale on kimmoisa, kuin golfpallo?
PG
Swinger: Näin siis tuo tukivoima ei pelkästään kiihdytä lavan ja pallon yhteistä massaa vaan painii tuota jousivoimaa vastaan. Ja, se ei olekaan lavan kiihdytys joka vaikuttaa pallon nopeuteen vaan toi jousivoima, ja tukivoiman vaikutus siihen.
Tarkoitatko, että osumassa vaikuttaa tukivoiman (F1) lisäksi jousivoima (F2), jolloin kokonaisvoima F = F1+F2? Ja tämä voima (F) vaikuttaa jollakin tavalla lavan ja pallon nopeuteen, jonka seurauksena pallo saa suuremman nopeuden ja vastaavasti lapa saa pienemmän nopeuden, kuin olen laskenut? (Esimerkeissämme tukivoima F1 on ollut 150 N. Käytetään sitä jatkossakin, mikäli jatkolaskenta on tarpeen. Jousivoiman F2 suuruutta ei tarvitse toistaiseksi tietää).
Joo ja ei. Golfpallon osumassa on jousivoimaa joka tapauksessa. Pallo puristuu kasaan, eli jousi menee kasaan ja se lisää jousen potentiaalienergiaa. Sitten kun jousi purkautuu, ko potentiaalienergia purkautuu taas jousivoimana takaisin. Käytännössä siis tuo jousi työntää törmääviä kappaleita koko ajan poispäin toisistaan, ja tekee sitä koko osuman ajan. Tuo F2 on siis jo mukana joka tapauksessa.
No, jos tähän tuo tukivoiman F1 mukaan, ja vain ’toisesta päästä’ jousta (lapa työntää palloa menosuuntaan). Tällöin lapa työntää sekä palloa että jousta yhtäaikaa. Ja, ajatus on siis se, että jousi painuu voiman F1 vaikutuksesta vähän enemmän kasaan kuin se muuten menisi (aikaansaaden sille isomman potentiaalienergian) ja jatkaa sitä vielä jousen purkautusvaiheessa. Tästä seuraa se, että jouselle tulee isompi voima kuin ilman F1 tukivoimaa. Ja, jousivoiman kasvaessa, jousi työntää palloa ja lapaa vähän voimakkaammin erilleen toisistaan kuin muuten kävisi. Ja edelleen, koska liikemäärän täytyy säilyä, ja jousi tunnetusti toimii niin että kevyempi saa tässä tilanteessa kovemman vauhdin kuin se painavampi kappale (ja tekee sen samassa ajassa eli myös pallon ja lavan kiihtyvyydet menee samassa suhteessa mutta eri suuntiin). Ja, lopputuloksena on tässä ajattelussa se, että lapa ja pallo ei mene yhtämatkaa kiihdyttäen eteenpäin, vaan niiden vauhdin muutos eroaa toisistaan tuon kasvaneen jousivoiman seurauksena.
Huom, en yritä ehdottaa että koko F1 (150N) menee tähän jousivoimaa vastaan painimiseen. Osa siitä on edelleen tuota lavan ja pallon yhteisen massan eteenpäin työntämistä.
PG: Vai tarkoitatko, että kaava F = ma ei päde, jos kappale on kimmoisa, kuin golfpallo?
Tokihan toi edelleen pätee. Tarkoitan, ja viittaan tässä aiempaan superpallon impulssikeskusteluun, tai siis siihen osaan niinkuin sen itse edelleen ymmärrän. Toi kimmoisuus (suurempi impulssi) vaikuttaa siihen että törmäys työntää kappaleita toisistaan poispäin eli kappaleiden välissä oleva jousivoima F=ma vaikuttaa kumpaankin kappaleeseen mutta eri suuntiin. Yhteensä liikemäärä säilyy.
Ei tukivoimaa
Kontaktin alkuosalla pallo puristuu kokoon => pallon jousienergia kasvaa. Tyhjästä ei energiaa nyhjäistä. Jousienergia otetaan kokonaisuudessaan siitä lavan liike-energiasta, joka lavalla osuman alussa on => lavan vauhti vähenee. Lisäksi lapa luovuttaa liike-energiaansa pallolle ’ihan sellaisenaan’ => lavan vauhti vähenee myös sitä kautta. (Voiman ja vastavoiman laki pätee, olkoon voima kotoisin mistä lähteestä tahansa).
Kontaktin loppuosalla jousen potentiaalienergia hyödynnetään => pallon vauhti kasvaa. Lavan liike-energiaa käytetään myös ’ihan sellaisenaan’ pallon vauhdin kasvattamiseen => lavan vauhti vähenee lisää.
Pallon liike-energia tulee siis osittain lavan liike-energiasta ja osittain jousen potentiaalienergiasta, mutta sekin otetaan lavan liike-energiasta. Lavan liike-energia -> pallon jousienergia -> pallon liike-energia.
Törmäyksessä liikemäärä säilyy, ts lavan liikemäärä + pallon liikemäärä on koko kontaktin ajan sama jokaisella ajanhetkellä.
Tukivoimatapaus
Pallo puristuu kokoon tässäkin tapauksessa, mutta siihen tarvittava energia saadaan tukivoiman tuottamasta energiasta, eikä osuman alussa olevasta mailanpään vauhdin energiasta. Sekä pallon, että lavan liike-energiat kasvavat tukivoiman takia koko kontaktin ajan. Pallo puristuu kontaktissa kokoon ja palautuu kontaktin lopussa ennalleen, mutta pallon saaman energian suhteen nollasummapeli. Riippumatta siitä, kuinka paljon pallo puristuu kokoon. Jos näin ei olisi, niin F=ma ei pätisi elastisille kappaleille. Aivan varmasti pätee. Kuten kaikki mekaniikan peruslait ja niihin nojautuvat kaavat, esim. Ft = mv, jossa F=ma. (Eri ämmät tähän tapaukseen sovellettaessa. Energiahäviöt eli energian muuttuminen ei toivotuiksi muiksi energiamuodoiksi on oma juttunsa).
Tukivoiman tuottama pallon ja lavan yhteenlaskettu liikemäärä kasvaa lineaarisesti koko kontaktin ajan.
Tukivoimatapaus on puhtaasti ’F=ma-tapaus’.
PG – kiitos. Fyysikko-minä ymmärtää sanomasi varsin hyvin ja vaikka golffari-minä vähän käkisteleekin vielä niin mieli palaa tällä hetkellä lyömään palloa ja pelaamaan, joten ehdotan että pannaan piste tälle keskustelulle.
Hyvä ehdotus. Kiitos, että otit asian uudelleen esiin kymmenen vuoden tauon jälkeen. Pari asiaa tarkentui minullekin.
Lyöntimme voi olla joskus ihmeellisen huono, mutta joskus ihmeellisen hyväkin. Syy molemmille aina sama: ihmeelliset luonnonlait.
”
Tämän itsestäänselvyyden puinnin sijaan mielenkiintoisempaa olisi miettiä pallon lineaarisen ja pyörimisnopeuden syntyä, joka on seurausta siitä, että mailanpään massakeskipisteen liikerata ei kulje pallon massakeskipisteen suuntaan vaan palloon kohdistuu sekä radiaalinen että tangentiaalinen komponentti.”Jos pallon ” kierreakseli” pysyy suunnassaan on lyönti hyvä. Jos se muuttaa suuntaansa niin pääosin lopputulos hukki tai slaissi. Kun se muuttaa suuntaansa sopivasti tulee draw fade.
Eräs pro sanoi että draw lyöntejä näkee harvoin mutta pikkuhukkeja usein…
Testailua eilen rauta-3:lla rangen nurmelta.
Aluksi lyöntejä ilman kummempia ajatuksia. Hieman osumat heitteli, tuli ohutta ja paksua osumaa ja huomasinkin että liioittelin liikettä hartioissa ylös/alas-suunnassa eli osuma-alueella oikeaa olkapäätä alas ja vastaavasti vasenta ylöspäin.Korjasin liikettä niin että kun oikea kyynärpää oli tullut lantion eteen niin tämän jälkeen hartiat pyörivät ennemminkin vaakatasossa (oikea olkapää luonnollisesti jo matalammalla kuin vasen). Tuloksena huomattavasti laakeampi lavan liike osuma-alueella ja sai pistää vauhtia pyörimiseen sen minkä pystyi.
Pallot lensivät melko suoraan ja pitkälle.En kuitenkaan ollut täysin tyytyväinen vielä pallon lentorataan, oli liikaa paraabelimainen!
Hieman pohdittuani muistelin opetettuja asioita ja kokeilinkin lisätä downsvingin alusta alkaen mailan lyöntiä/vetoa alaspäin oikealla kädellä niin että lapa putoaa selän taakse ja liike tietenkin jatkui niin että oikea kyynärpää yhä tuli lonkan eteen.
Liike oikealla kädellä lähes sama kuin kivellä leipiä heittäessä.Nyt palaset loksahtivat yhteen. Käsillä sai lyödä täyttä ja hartioilla pyöriä niin nopeasti kuin vanhasta kropasta lähtee.
Se mikä eniten ilahdutti oli että pallon lentorata muuttui merkittävästi.Nyt pallot näyttivät lähtevän matalammassa kulmassa ja kiipeävän ylöspäin ikäänkuin koveralla kaarella ja lopussa tullen alas jyrkemmin.
Herätti toiveita että saisi pallon pysähtymään griinille pidemmilläkin par-3:llaPs. Liittyy tähän ketjuun koska voiman käyttö/lisääminen oli järkevää vasta noiden ahaa elämysten jälkeen.
Mutta se pyörii sittenkin…?!
Kausi alkaa olemaan lopuillaan, ja lueskelin tän ketjun uudestaan läpi. Pari kolme havaintoa tuli mieleen, sekä tästä keskustelusta että omasta lyönnistä kesän mittaan. En tiedä onko aihe jo loppuun kaluttu, mutta talvi on sopivaa aikaa resonoinnille jos sille löyty vielä kiinnostusta.
Yksi fundeerauksen kohde on ollu se, että onko yleisesti paljon käytetty ohje ’kiihdytä läpi osuman’ vain mielikuva vai myös todellinen. Mun oma kokemus puhuu kyllä selvästi sen puolesta että ohje on todellinen eli näin kannattaa todellakin tehdä. Ja kiihdytys tarkoittaisi tietysti sitten myös että osuman läpi on voimaa mukana. Tämä on siis empiirinen mutu.
Katselin myös sen ns korealaistutkimuksen läpi uudestaan ja mun mielestä myös sen tuloksissa näkyy kiihdytys läpi osuman. Ei ehkä suoraan mutta kyllä se siellä on. Tämäkin vahvistaa mun käsitystä että osuman läpi käytetään kiihdystä ja siis voimaa. Laitan linkin siihen tässä uudestaan ettei tarvi kahlata koko ketjua läpi löytääkseen sen: Tutkimus
Toinen huomio on oikeastaan pariosainen kysymys, josta eka osa menee PG:lle.
Olin kopioinu PG:n vastauksen 11.12. viime vuonna (liittyen osuman rekyyliin) näin:
PG
Palaan vielä tuohon voiman ja vastavoiman lakiin.Perustilanne ilman ulkoista voimaa: lapa vaikuttaa palloon voimalla F => pallo vaikuttaa lapaan voimalla F.
Lisätään sitten mukaan ulkoinen voima ΔF.
Nyt lapa vaikuttaa palloon voimalla F + ΔF => pallo vaikuttaa lapaan voimalla F + ΔF.
Mitä se merkitsee?
Sitä, että pallon lähtönopeus kasvaa ja lavan nopeus hidastuu perustilanteeseen verrattuna. Ja samalla myös sitä, että ulkoisella voimalla ei voida rekyyliä vähentää. Päinvastoin se kasvaa.
Huomasin sitten että PG:n alkuperäisessä tekstissä ei enää (myöhemmin) ollu noita paria viimeistä kappaletta, ja esim tuo kommentti pallon lähtönopeuden kasvusta ja lavan hidastumisesta oli poistettu (editoitu PG:n toimesta?). Oliko näin ja oliko tuossa tekstissä joku vika?
Huomio taas liittyy siihen että myöhemmin juteltiin rautamailojen deloftauksesta ja mun ymmärtääkseni siinä tapahtuu sama, eli lapa hidastuu enemmän ja pallo saa vastaavasti isomman lähtönopeuden. [Niissä pidemmissä kaavoissahan on kosiniarvo kulmasta ja kulman muuttuessa cos:kin muuttuu mikä kaiketi johtaa voimien vaikutuksenkin muuttumiseen edellä mainitulla tavalla.]
Mistä taas seuraa se, että kahdessa samavauhtisessa lyönnissä (pallon nopeuden kasvaessa ja lavan hidastuessa) myös COR-arvo muuttuu ja samaten smash factor – riippuen miten palloa lyödään, esim deloftaamalla tai ilman. Meniköhän tää fundeeraus oikein?
onko yleisesti paljon käytetty ohje ’kiihdytä läpi osuman’ vain mielikuva vai myös todellinen.
Riippuu siitä, kumpaa ohjeen esittäjä on tarkoittanut. Yleensä kai tavoitteena kuitenkin on saada mailanpäälle maksimivauhti pallon kohdalla. (Tällöinhän mailanpään kiihtyvyys on nolla). Osuman läpi lyöminen tai osuman läpi vieminen taitavatkin olla yleisempiä ohjeita kuin ohje osuman läpi kiihdyttämisestä. Esim. Heini Haapala:
Hyvä golfsvingi ei lopu osumaan. Vauhti pyritään pitämään mailan lavassa läpi lyönnin, jolloin voima siirtyy osumassa palloon kuin vahingossa.
Samoilla linjoilla näyttää olevan myös PeGo:
Vie läpi (follow through). Liike viedään osuman läpi eli jos olet tehnyt liikkeet hyvin, vie swingi sinut tasapainoiseen loppuasentoon.
Antti Vaalas puolestaan kehottaa kiihdyttämään tasaisesti osumaan (ei osuman läpi), mutta antaa silti ohjeeksi: ”Jotta vauhti kiihtyisi osumaan, pelaajan kannattaa ottaa tavoitteekseen tuntea lavan vauhdin olevan nopeimmillaan vasta pallon jälkeen. Näin todellisuudessa paras vauhti ajoittuu todennäköisesti lähemmäksi osumakohtaa.”
Tuo on varmaan totta. Vaikka mailanpään vauhti romahtaakin draiveriosumassa jopa yli 30 %, silti mailanpään nopeus voi tuntua olevan suurimmillaan vasta osuman jälkeen. Kyse on siis mielikuvasta.
Ja kiihdytys tarkoittaisi tietysti sitten myös että osuman läpi on voimaa mukana.
Kyllä, mutta kannattaa muistaa, että vielä enemmän voimaa on mukana sellaisessa svingissä, jossa mailanpää saavuttaa suurimman vauhtinsa jo pallon kohdalla (siis ilman osuma-aikaista kiihdytystä).
Mun oma kokemus puhuu kyllä selvästi sen puolesta että ohje on todellinen eli näin kannattaa todellakin tehdä.
Tekemisessäsi saattaa olla kyse Vaalaksen ohjeen mukaisesta asiasta: paras vauhti on lähellä osumakohtaa, vaikka tuntuukin olevan paljon myöhemmin. Tai kenties tuolla tekniikallasi saat toistettavampia lyöntejä ja parempia osumia. Jos näin on, niin mielestäni tekniikkasi on hyvä.
Huomasin sitten että PG:n alkuperäisessä tekstissä ei enää (myöhemmin) ollu noita paria viimeistä kappaletta, ja esim tuo kommentti pallon lähtönopeuden kasvusta ja lavan hidastumisesta oli poistettu (editoitu PG:n toimesta?). Oliko näin ja oliko tuossa tekstissä joku vika?
Tarkkana olet ollut. Poistamassani tekstissä oli todellakin vikaa. Lavan nopeus ei tuossa vähene. Ulkoinen voima ΔF (eli lapaa ja palloa osuma-aikana kiihdyttävä ”tukivoima”) kasvattaa sekä lavan että pallon nopeutta yhtä paljon.
(Tarkennus: Jos jätetään lavan lyöntipinnan vähäinen joustaminen huomioonottamatta, lavan kontaktiaikainen nopeuden kasvu on lineaarista. Sen sijaan pallon kokoonpuristumisesta ja palautumisesta johtuen pallon massakeskipisteen nopeuden kasvu on epälineaarista: sen nopeus kasvaa aluksi hitaammin kuin lavan, mutta myöhemmin nopeammin. Kuitenkin kontaktin lopussa ”tukivoiman” ΔF aiheuttama nopeuden lisäys on lavalla ja pallolla täsmälleen samansuuruinen. Ks. 7.4.2021 13:15:27 graafi ylhäällä vasemmalla.)
Lisäksi katsoin rekyylikäsitteen olevan liian laajan ja liittyvän paremminkin aseisiin ja on mielestäni golflyönnin kannalta varsin epäoleellinen asia.
myöhemmin juteltiin rautamailojen deloftauksesta…. Meniköhän tää fundeeraus oikein?
Ihan oikein meni.
Hyviä poimintoja osuman läpi kiihdyttämisestä / voiman käyttämisestä…!
Lapahan hidastuu joka tapauksessa osumassa, joten siltä osin ajatus että vauhti olisi suurimmillaan (heti) osuman jälkeen on toki väärin. Se osa on ilman muuta ’vain’ mielikuva. Se että kannustetaan kiihdyttämään osuman läpi on taas mun mielestä oikein koska se saa pelaajan tekemään oikeita asioita. Osin muuten tähän samaan asiaan pieni jatko keväältä:
PG
Swinger?
Lisäksi, kaikki hyvät pallonlyöjät ovat väärässä vaikka osaavat palloa lyödä hyvin.Miten tuo liittyy tähän asiaan?
jäi näköjään silloin vastaamaatta tähän, mutta tähän samaan ’kiihdytys osuman läpi’ asiaan toi mun heitto liittyi.
Tän aasinsillan perään voisinkin jatkaa vielä kolmannen ajatuksen, ja oikeastaan vähän ihmetyttää että onko tää itsestäänselvää tai miten se ei aiemmissa jutuissa tullu keskustelun kohteeksi(?).
Keskipakovoimahan on verrannollinen lavan nopeuden neliöön, ja kun tässä on puhuttu että lavan nopeus ratkaisee ja jos haluaa pallolle lisää nopeutta niin se tulee lavan nopeuden lisäämisen kautta. Ja, lavan nopeutta kiihdyttämällä siis myös keskipakovoiman suuruus kasvaa. Ja, jos ei halua sokettia tai kuokkalyöntiä, niin pelaajan täytyy kasvattaa sille vastavoimia (ja/tai tehdä vastaliikkeitä mihin myös tarvitaan jotain voimia). Kohdistuu lyhyeen ajanhetkeen, mutta aika isosti.
Mistä siis tulee se varsin suora johtopäätös että lavan vauhdin kasvaessa täytyy lisätä voimaa. Ja tavoite on kai saada noi molemmat suurimmilleen osumassa. Osuma on kestoltaan todella lyhyt (se n. sadasosa silmänräpäyksestä), joten luultavasti ainoa oikea tavoite on viedä ko voimankäyttö osuman läpi.
Muuten, näin ajatellen, jos jutun otsikko on ylipäätään ’voimaa osumaan’ niin eiköhän tämäkin huomio kuulu saman otsikon alle? Lisänopeus osumassa tarkoittaa varsin suoraan myös tarvetta lisätä voimaa?
Ainakin oma kokemus on se, että kun noita vastavoimia/vastaliikkeitä oppii tekemään/käyttämään, niin voi lisätä mailan ja lavan kiihdyttämistä. Mikä taas lisää ko vastavoimien tarvetta… mutta kehitysluuppi on silloin oikeansuuntainen? ’Dig it from the dirt’?
-
JulkaisijaArtikkelit
Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros