Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros
-
JulkaisijaArtikkelit
-
Siis
v = (1 + COR)V/(1 + m/M) + Fdt/(m+M)
eli
vball = (1 + COR)*vclub/(1 + mball/mclub) + F*t/(mball+mclub)
Kyllä se näin on. Kysymys kuuluu vain, miksi se on näin. Jos jotakuta se sattuisi kiinnostamaan, niin voisin selittää…
Kun sitä tukivoimaa on niin tuo kaavan pikku t kasvaa.
Kuinka paljon sitä on oltava kun r5 pallon lento 160m lisääntyy 20m?
Mailanpään vauhdin pysyessä samana palloa lyötäessä. Ilman palloa nopeus olisi kyllä suurempi.Pikku t ei tarvitse niin mahdottomasti kasvaa?
Näprääjä
Kun sitä tukivoimaa on niin tuo kaavan pikku t kasvaa.
Kuinka paljon sitä on oltava kun r5 pallon lento 160m lisääntyy 20m?Erittäin hyvä kysymys.
Jotta pallo lentäisi 20 m pitemmälle, pikku t:n (joka PT:n liikemääräyhtälössä on dt) tulisi olla 0,0077 sekuntia eli 15 x kontaktiaika. Ei siis onnistu (kun F = 150 N ja M=300g). Lentomatka kasvaa vain 1,3 m, vaikka tukivoima on todella iso.
(Perustelut: Yleensä lasketaan, että pallon lähtönopeuden lisäys 1 mph:lla lisää pallon lentomatkaa 3 jaardilla eli 2,7 m:llä. Kontaktiaikana (t =0,0005 s) pallon nopeus lisääntyy määrällä F*t/(m+M) = 150*0,0005/0,346 m/s = 0,22 m/s = 0,48 mph. Se on vain 1/15 tarvittavasta nopeudesta.)
Jos pallo kontaktissa 0.1 sek niin ehtisi siirtyä energia hyvin. Yhdessä kuljettu matka 0.04 m ka nopeus vaikka 30 m /sek? Alkaa olemaa liki noilla ?
Täytyy sanoa etten ole kovin innostunu noista COR-pohjaisista kaavoista. Jotta niitä voisi käyttää pitää tietää oikea arvo COR:lle, ja siihen taas tarvitaan mm. pallon nopeus osuman jälkeen. Jos sitten syöttää kaikki arvot ko kaavaan, ja laskee sillä mikä on pallon nopeus osuman jälkeen, niin ei-niin-yllättäen siitä pitäisi tulla vastaukseksi sama luku kuin jo tiedettiin lähtöarvojen perusteella. Joten, vaikka laskukonetta tai Exceliä voi olla kiva käyttää niin ei taidettu oppia mitään uutta.
Laskin COR arvot tuosta mun R7 esimerkissä. Ilman tukivoimaa COR on 0.48 ja 150N tukivoimalla 0.51.
Se sääntöjen määräämä maksimiarvo COR:lle koskee mailan sääntöjenmukaisuutta. Palloa ammutaan lapaan ja mitataan ettei mailan lavan (materiaalien) jousivoima/trampoliiniefekti ole suurempi kuin COR 0.83. Mutta, ei säännöissä ole mitään maksimiarvoa golf-lyönnin COR-arvolle. Newtonilla on sille oma mielipiteensä, mutta se on eri juttu.
Alkuperäiset laskelmat tehtiin tyyliin ’jos jousivoimaa ei oteta huomioon’. No, ne kuitenkin pitää ottaa mukaan. Ehtiikö pallo puristua ja palautua osuman aikana? Kuvista päätellen ehtii. Ehtiikö tukivoima lisätä liikemäärää osuman aikana? Pienen määrän kyllä ja se työntää sekä palloa että lapaa menosuuntaan. Ja, samalla pallo puristuu vähän enemmän kasaan ja sitten työntää lapaa ja pallo erilleen toisistaan jousen purkautuessa. Säilyykö liikemäärä tuosta huolimatta? Kyllä. Miten se jakaantuu? Siten että nopeudet muodostuvat jousen purkauduttua pallon ja lavan massojen suhteessa. Pallo saa siis (ko voiman vaikutuksen osalta) n. 6.5 kertaisen nopeuden kuin lapa (arvoilla lapa 300g ja pallo 46g), ja ne tapahtuu samassa ajassa joten kiihtyvyydetkin menee samassa suhteessa.
Osumassahan pallo kiihtyy kovaa muutenkin ja lapa hidastuu, joten tuo tukivoima sitten kiihdyttää palloa vähän enemmän ja vastaavasti lapa hidastuu vähän vähemmän. Lisäksi, osumassa osa energiasta muuttuu lämmöksi, ääneksi, spinniksi jne, ja suurin osa siitä tapahtuu tietysti ilmankin tuota tukivoimaa. Jos tarkkaan haluaisi laskea miten kaikki tapahtuu, niin noi pitää ottaa mukaan, ja käyttää Hertzin jousivoimaa ja muita tekijöitä. Sen jätän kuitenkin muille, omalta osaltani yo peruslogiikka tapahtumista riittää.
Muilta osin tää keskustelu ei taida tulla valmiiksi. Kevätkin edistyy ja kentät aukeaa, joten taidan siirtyä tutkimaan tätä asiaa käytännön puolelle. Talven spekuloinnit osuman voimista taitaa riittää pikkuhiljaa.
Näprääjä
Jos pallo kontaktissa 0.1 sek niin ehtisi siirtyä energia hyvin. Yhdessä kuljettu matka 0.04 m ka nopeus vaikka 30 m /sek? Alkaa olemaa liki noilla ?Jos kontaktiaika on 0,1 s, niin kyseessä ei ole golflyönti vaan flippaus, jossa alkutilanteessa mailanpää lepää paikallaan pallon takana, eli sillä ei ole mitään vauhtia. Kuten alla:
Swinger 3.12.2020 12:03:18
Oletetaan että pelaaja lyö rautaseiskalla 150m ja tuo tulee puhtaasti mailanpään vauhdista. Laitetaan rinnalle tilanne jossa mailanpää lepää paikallaan pallon takana, eli sillä ei ole mitään vauhtia. Voiko pelaaja kyseistä tilanteesta laittaa pallon liikkelle? Vastaus kai liene ilman muuta selvä, totta kai voi. Ranteilla voi vipata esim 10 metriä, ottamalla vähän käsivarsia mukaan ja miksei myös vähän vartaloa ja lantiota, ja myös tukeutumalla takajalan varaan luultavasti aika paljon enemmän. Jonkun verran treeniä varmaan tarvitaan jos haluaa tuon vielä onnistuvan hyvin, mutta voisin kuvitella että treenaamalla voisi päästä esim 50 metriin. Ja, tämä siis ilman mitään mailanpään vauhtia osumassa, eli pelkällä voimalla. Tuon teorian mukaan jossa vain mailanpään vauhti ratkaisee tämän ei pitäisi olla mahdollista…?Kyllä flippaaminen mahdollista on, mutta golflyönniksi sitä ei hyväksytä. Voidaan silti laskeskella.
Oletetaan, että tuossa flippauksessa F = 150 N, M = 300 g ja kontaktiaika t=0,1 s. Pallon ja lavan nopeus kontaktiajan lopussa on 43,4 m/s ja keskikiihtyvyys molemmille 434 m/s^2. Yhdessä kuljettu matka 2,17 m. (Käytännössä ihan näin pitkä kontaktimatka ei taida onnistua, eli voimaa pitäisi vähän vähentää).
P.S. Tätä flippaamisesimerkkiä voidaan soveltaa myös golflyöntiin, jossa mailanpäätä kiihdytetään 150 N voimalla osuman läpi. Jos kontaktiaika on 0,5 ms, niin lavan ja pallon nopeuden kasvaminen osuman aikana on tietenkin 0,0005/0,1*43,4 m/s eli 0,22 m/s = 0,48 mph. Mukaan ei tarvitse (eikä pidä) sotkea mitään muuta. Superpositioperiaate pätee (= voidaan analysoida eri tilanteita yksittäisinä tapauksina ja vasta lopuksi yhdistää ne kuvaamaan monimutkaisempaa tilannetta).
Kuulehan Swinger: antamissani epäelastisen törmäyksen liikemäärän ja energian säilymislaeissa on otettu huomioon jousivoimat (ja dashpot). Jousivoiman, tai tarkemmin jousivakion vaikutus tulee kokonaisuudessaan sekä vain ja ainoastaan kontaktiajan kautta.
Liikemäärän ja energian on säilyttävä törmäyksessä tai muuten syntyy ikiliikkuja. Nämä kaavat on aika lailla koeteltua kamaa (liikemäärän säilyminen: Newton n. 1700; energian säilyminen William Rankine n. 1850).
Driverin jousivakiohan on säännöissä rajoitettu, koska karakteristinen aika on rajoitettu 239 mikrosekuntiin (ei siis COR -rajoitusta). Karakteristinen aika määritetään teräskuulalla eli erittäin suurella ”pallon” kimmomoduulilla niin, että mailan ja kuulan kimmomoduulien muodostaman kokonaisuuden kimmomoduuli on täysin mailan määräämä. Rautamailojen kimmomoduuli on suurempi kuin driverin, joten rautamailan ja golfpallon törmäyksen kimmomoduuli on pallon määräämä ja edelleen rautamailan ja pallon kontaktiaika on siis lyhyempi kuin driverin ja pallon kontaktiaika.
Äkkiä googlaamalla löysin yhden artikkelin vuodelta 2001 (Roberts et al Sports Engineering 4 (4): 191-203), jossa on tutkittu kontaktiaikaa tuon ajan, v. 2001, drivereilla, joilla kontaktiaika on lyhyempi kuin nykyisillä, mutta pidempi kuin raudoilla. Varmaan, Swinger, luet tämän artikkelin huolellisesti (löytyy ilmaiseksi), mutta spoilataan nyt sen verran, että tulokset liikkuvat siellä suuruusluokassa 0.5 ms (mitä arvoa PG onkin käyttänyt) vaihdellen vähän pallon kovuudesta ja mailanpään nopeudesta riippuen.
Eli sorry, Swinger, fysikaalisesti olet valitettavasti täysin hakoteillä (kuten joskus aiemmin yritin sanoa nätisti), joten siirtyminen käytännön harjoituksiin kuulostaa hyvältä suunnitelmalta. Minulla se käytännön puoli on vähän huonoa, mutta aion kuitenkin yrittää – jatkaen sitä hyvää perinnettä mitä olen noudattanut vuodesta 1985: prolla ei käydä (ne kun ei osaa laskea liikemääriä ja energioita puhumattakaan monimutkaisemmasta dynamiikasta). Jokainen fyysikko tietää, miten golfpalloa pitää lyödä – valitattavasti fyysikoiden lihakset ja hermotukset eivät tiedä, miten se toteutetaan…
Hyvää pelikautta!
PappaTykki
artikkelin vuodelta 2001 (Roberts et al Sports Engineering 4 (4): 191-203), jossa on tutkittu kontaktiaikaa tuon ajan, v. 2001, drivereilla, joilla kontaktiaika on lyhyempi kuin nykyisillä, mutta pidempi kuin raudoilla. Varmaan, Swinger, luet tämän artikkelin huolellisesti (löytyy ilmaiseksi), mutta spoilataan nyt sen verran, että tulokset liikkuvat siellä suuruusluokassa 0.5 ms (mitä arvoa PG onkin käyttänyt)Joo olen lukenu, siihen on tässä ketjussa jo aiemmin viittattukin, ja samaa 0.5ms arvoa ollaan PG:n kanssa käytetty osuman kestosta. Siinä tutkimuksessahan todettiin myös että osuma vähän lyhenee kun driverin vauhti kasvaa ja Hertsin jousestakin siinä puhuttiin. Eli on tuttu kyllä. Samaten Pennerinkin luin aiemman pyyntösi mukaisesti.
PappaTykki
Liikemäärän ja energian on säilyttävä törmäyksessä tai muuten syntyy ikiliikkuja.Liikemääriä ollaan enimmäkseen laskettu, mutta kaikissa laskelmissa ne täytyy tosiaan säilyä. Tätä periaatetta olen itsekin noudattanu. Energioita en ole erikseen tarkastanu, ja ylipäätään olen laskeskellu lähinnä approksimaatioita suuruusluokkamielessä. PG on pahimmat ajatusmokat onnistuneesti korjannu (niitäkin on tosiaan mukana ollu ja ne olen myös noteerannut), mutta ensisijaisesti ollaan päädytty lisävoimalla lisäämään lavan ja pallon yhteistä liikemäärää (sen ’normaalin osuman’ lisäksi), ja sitten pidetty huolta että sama kokonaismäärä säilyy. Pallon jousivoiman vaikutuksesta ei taidettu kuitenkaan päästä tällä erää valmiiksi.
Hyvää pelikautta!
Kuin myös! Jos asia vielä tuntuu kiinnostavalta myöhemmin niin jatketaan kauden jälkeen.
Vähän pitkä flippaus 😅
Mites ajatus jos pallo puristuu kokoon 1 cm ja toinen 2 cm? Toisen ” kimmovoima” pienenmpi. Metrejä lisää?
Se vähän riippuu…
Kevätkin edistyy ja kentät aukeaa, joten taidan siirtyä tutkimaan tätä asiaa käytännön puolelle.
Tässä kesäksi mietittävää.
ei säännöissä ole mitään maksimiarvoa golf-lyönnin COR-arvolle.
Ei, mutta millä konstilla 0,83 pystytään ylittämään? Läpi osuman kiihdytyksellä se ei onnistu.
Laskin COR arvot tuosta mun R7 esimerkissä. Ilman tukivoimaa COR on 0.48 ja 150N tukivoimalla 0.51.
Sekä lavan että pallon nopeudet kasvavat lyönnissäsi 0,22 m/s. COR ei siis muutu. Molemmissa tapauksissa se on 0,49. Sen sijaan smash factor kasvaa, mutta ero näkyy vasta 3. desimaalissa (1,286->1,292).
Joo olen lukenu,…. Samaten Pennerinkin luin aiemman pyyntösi mukaisesti.
Luepas vielä tämä: https://www.tutelman.com/golf/swing/accelerateThru.php. Sen mukaan ’tukivoima’ on yhtä tyhjän kanssa. Jutusta selviää hyvin myös se, että ’tukivoiman’ tuottaman nopeuslisän laskemisessa voidaan käyttää keskimääräistä voimaa, olkoon voimaprofiili F=F(t) millainen hyvänsä.
Voiman ja vastavoiman laki pätee sekä hetkelliselle että keskimääräiselle voimalle. Keskimääräistä voimaa käytin alla olevassa tarkastelussani ketjussa Mailanpään hidastuvuus. Jos hyväksyy voiman ja vastavoiman lain, on hyväksyttävä myös tarkatelun lopputulos.
PG kirjoitti: (1.3.2011 21:34:28)
Oletetaan, että osumassa vaikuttaa myös ulkopuolinen voima F. Lapaan vaikuttaa silloin voima F + lavan_massa*lavan_nopeuden_muutos/kontaktiaika. Palloon vaikuttava voima on pallon_massa*pallon_nopeuden_muutos/kontaktiaika. Voiman ja vastavoiman lain perusteella saadaan
F + mclub*[(vclub –Vclub)/t] = mball*[vball/t]
Kertomalla yhtölö t:llä saadaan
F*t + mclub*(vclub – Vclub) = mabll*vball
Otetaan COR mukaan. Ratkaisu menee kuten aiemmin ilman ulkopuolista voimaa. Lopputulos on muuten sama kuin ilman ulkopuolista voimaa, mutta lisälausekkeeksi tulee F*t/(mclub + mball). Siis
vball = (1 + COR)*vclub/(1 + mball/mclub) + F*t/(mclub + mball)
Jos mailanpään kiihtyvyys on 200 m/s^2 (eli peräti 20 geetä!), niin lapaan kohdistuva voima F on lavan massa*kiihtyvyys, noin 40 N. Se kasvattaa pallon nopeutta vain noin 8 cm/s. Muskelivoima ja varren jousivoima pitää siis käyttää jo ennen osumaa. Osumassa niiden merkitys on mitätön.
Voimat mclub*[(vclub –Vclub)/t] ja mball*[vball/t] ovat osuma-aikaisia keskimääräisiä voimia. Vakiovoiman F keskiarvo on F. ’Tukivoiman’ tuottama nopeus F*t/(mclub + mball) ei sisällä COR-termiä. Se tarkoittaa, että pallon kimmoisuudella ei ole väliä. Sama vauhdin lisäys, olkoon COR 0 tai 1 tai jotain siltä väliltä. Kontaktiaikana palloon kohdistuva keskimääräinen voima (=20 N, jos F=150 N ja m=300 g) sisältää myös jousivoiman ja ratkaisee yhdessä kontaktiajan kanssa sen, kuinka suuren nopeuslisän tukivoima tuottaa.
Swinger: Jousi toimii niin että molempia tulee työnnettyä yhtä paljon ja samassa ajassa eroon toisistaan, eli molemmat saavat saman liikemäärän. Tällöin myös massakeskipiste jatkaa menoaan oikealla vauhdilla. Ja, jos molemmat saavat saman p=mv, niin pallo saa sitten massojen suhteessa isomman vauhdin jotta tuo liikemäärän säilyminen tapahtuu.
Jos massojen suhde on 300g vs 46g, niin pallo saa n. 6.5 kertaa isomman vauhdin; ja aikaisemmalla R7 esimerkillä pallo saa 0.812m/s lisää vauhtia ja lapa 0.125m/s.Jotta tuo teoria pitäisi paikkansa, sen tulisi toimia kaiken painoisilla palloilla ja lavoilla (riippumatta siitä ovatko ne golfin sääntöjenmukaiset). Nähdään helposti, että näin ei ole. Tuon teorian mukaan lapa, pallo ja palloon kiinnittynyt elastinen hyttynen saisivat kukin kolmanneksen yhteisestä liikemäärästä. Kesätehtävä: kuinka suuren vauhdin lapa, pallo ja hyttynen saavat?
Hyvää kesää!
PG
Luepas vielä tämä: https://www.tutelman.com/golf/swing/accelerateThru.php. Sen mukaan ’tukivoima’ on yhtä tyhjän kanssa.Otetaas tähän pari esimerkkiä.
1. Pallon ja lavan välissä on vieteri, kaikki on paikallaan. Lapaa työnnetään voimalla X sen aikaa kun vieteri puristuu ja sitten vapautuu. Kitkaa ei ole. Onko pallolla ja lavalla sama vauhti kun vieteri on purkautunut? Ei ole, pallolla on kovempi vauhti.
2. Sama mutta ilman vieteriä. Sama voima ja sama kesto. Pallo ja lapa liikkuvat yhtä matkaa joten nyt niillä on sama vauhti lopussa.
Tutelman laskee tilanteen tuolla tavalla 2. Todellisuudessa siinä on kuitenkin tuo jousi välissä [golf-pallon puristuminen osumassa], joten lopputuloskin on eri. Eikä toi edellä kuvattu tilanne (tai noiden kahden testin ero) muutu siitä miksikään vaikka lavalla olisi jo tuohon tilanteeseen tullessa vauhti päällä.
Tässä voidaan ohjata keskustelua siihen suuntaan että olen laskenut tuon väärin. Ei se mitään, omista opinnoista on jo pitkä aika eikä mun mielenkiinto riitä tuon täsmälliseen laskemiseen. Eli, mahdolliset laskuvirheet ei haittaa mua itseäni. Eikä se tarkempi tieto muuttaisi mun golf-swingiä mitenkään. Sen sijaan ymmärrys siitä mitä osumassa tapahtuu late hitting:n seurauksena kyllä muuttaa. Joten, keskityn siihen. Tutelman sen sijaan tekee isomman virheen kun ei ota tuota ollenkaan huomioon. Enkä enää tiedä miten saataisiin päivä paistamaan tähän risukasaan.
Lyhyesti, en usko Tutelmania. Uskon itseäni. Hyviä swingejä kaikille.
Osan aikaa tämä keskustelu on ollut ihan mielenkiintoista ja viihdyttävääkin. Kiitos siitä; varsinkin PG ansaitsee tunnustuksen sitkeydestä. Viimeaikoina olen kuitenkin ollut havaitsevinani viestinnässä päättymättömän luupin.
Tutelmania mukaellen: ”When all you have is a spring, you tend to treat everything as a …”Itse aion keskittyä seuraavaan DT:n sanomaan:
Every golf instructor I’ve ever read or heard says you must accelerate through impact. Then they extend this advice to mean that you will hit the ball farther — more ball speed — because you are accelerating the clubhead through the ball, than if you were simply coming into the ball at a constant clubhead speed. The first is good instruction. The second is not good physics.Swinger:
OK, mutta katotaas sitä flippausesimerkkiä vielä uudelleen.
Alkutilanteessa (hetkellä t=0) mailanpää on pallossa kiinni paikallaan pallon takana. Flipataan 150 N voimalla. Lavan massa 300 g ja kontaktiaika t=0,1 s. Edit: Oletetaan, että pallon kokoonpuristuminen on maksimissaan hetkellä t = 0,00025 s.
Mitkä pallon ja lavan nopeudet ovat hetkilläa) t = 0,00025 s
b) t = 0,05 s (eli puolivälissä)
c) t = 0,09975 s (eli 0,00025 s ennen kontaktin loppumista)
d) t = 0,1 sKuinka suuri kokonaisvoima (’tavallinen voima’ ja jousivoima yhteensä) em. hetkillä palloon vaikuttaa?
4par
Viimeaikoina olen kuitenkin ollut havaitsevinani viestinnässä päättymättömän luupin.Samaa mieltä, ei tästä valmista tule. Ollaan korkeintaan yhtä mieltä siitä että ollaan eri mieltä. Tarkoitus on ollu jo hetken aikaa lopettaa koska tää ei etene enää mihinkään.
4par/DT
Every golf instructor I’ve ever read or heard says you must accelerate through impact. Then they extend this advice to mean that you will hit the ball farther — more ball speed — because you are accelerating the clubhead through the ball, than if you were simply coming into the ball at a constant clubhead speed. The first is good instruction. The second is not good physics.Selvyyden vuoksi: Tutelman, PG ja minä ollaan samaa mieltä ettei lavan kiihdytys ole se juttu, koska osuman kesto on niin lyhyt. Kiihdytyksen vaikutus on marginaalinen, eli niin pieni ettei oleellisesti vaikuta. Se mistä ei olla samaa mieltä on se, että ko tukivoima antaisi pallolle ja lavalle täsmälleen saman määrän lisänopeutta osuman lopussa. Pallon puristuminen / jousivoiman mukaantulo / ’superpalloimpulssi’ muuttaa tuota tilannetta.
PG:lle: kiitos ehdotuksista ja vinkeistä – en tosin ala laskemaan uusia laskuja.
Minullakin olisi kyllä edellytyksiä koulutukseni ansiosta laskeskella noita osumaan liittyviä voimia. Näen kuitenkin mielekkäämmäksi tutkiskella asiaa käytännön näkökulmasta joka myös voi tuoda glubigolffareille auttavia mielikuvia.
Itse sain erinomaisen käytännön opin aiheesta nyt jo edesmenneeltä entiseltä maajoukkuepelaajalta noin 30 vuotta sitten eli hän vinkkasi seuraavaa: tee swingejä korkeahkossa heinikossa niin että maila menee siitä läpi.
Oheinen temppu onnistuu juurikin vain niin että veto pysyy päällä koko swingin ajan! Jos lopetat vedon ja annat mailan tehdä heiluriliikkeen niin lapa pysähtyy takuuvarmasti heiniin.Mielestäni tuo vanhan kansan neuvo ”kiihdytä läpi osuman” on vain mielikuva ja tarkoittaa oikeammin juurikin sitä että on tärkeää pitkä veto päällä läpi osuman.
”Tavallisen glubigolffarin” swingin voisi kuvailla niin että vedetään kyllä maila palloon ja annetaan sen sitten heilahtaa läpi osuman. Tämän jälkeen swingi jatkuukin niin että maila vetääkin käsiä loppuasentoon. Osumassa vaikuttaakin näin ”vain” heilahtavan mailan massa jolloin myös lavan hidastuvuus osumassa on huomattavasti suurempi kuin pelaajalla jolla veto pysyy päällä koko osuman ajan eli toisin sanoen tuottaa juurikin myös sitä paljon puhuttua tukivoimaa.
Mielestäni ylläolevassa on koko osuman voimantuoton perusidea puuttumatta siihen mitä käskytyksiä kropassa on tehtävä!
PeWin
Osumassa vaikuttaakin näin ”vain” heilahtavan mailan massa jolloin myös lavan hidastuvuus osumassa on huomattavasti suurempi kuin pelaajalla jolla veto pysyy päällä koko osuman ajan eli toisin sanoen tuottaa juurikin myös sitä paljon puhuttua tukivoimaa.Tarkoitatko, että mitä suurempi lavan hidastuvuus osumassa on, sitä pienemmän lähtönopeuden pallo saa!?
Selvyyden vuoksi: Tutelman, PG ja minä ollaan samaa mieltä ettei lavan kiihdytys ole se juttu, koska osuman kesto on niin lyhyt. Kiihdytyksen vaikutus on marginaalinen, eli niin pieni ettei oleellisesti vaikuta.
Kantasi on siis ketjun aikana muuttunut. Hyvä!
Se mistä ei olla samaa mieltä on se, että ko tukivoima antaisi pallolle ja lavalle täsmälleen saman määrän lisänopeutta osuman lopussa.
PG:lle: kiitos ehdotuksista ja vinkeistä – en tosin ala laskemaan uusia laskuja.
Ei kestä. Tarkka laskeminen ei ole tarpeenkaan. Tärkeintä on ymmärtää, että pallon kokoonpuristaminen kontaktin alussa vaatii energiaa, joka muuttuu pallon jousienergiaksi, joka sitten kontaktin lopussa saadaan suurimmaksi osaksi takaisin liike-energian muodossa. Ikiliikkujaa ei synny. ’Tukivoiman’ aiheuttaman kokoonpuristumisen jälkeen pallo ja lapa kulkevat tuossa esimerkissä samalla kiihtyvällä nopeudella – pallo kokoonpuristuneena jousienergialla varustettuna.
Esimerkin tapauksessa kiihdyttävä voima lavalle ja pallolle on yhteensä 150 N. Koska yhdessä menevät, niin lapaan kohdistuu 130 N ja palloon 20 N (muuten joutuisivat toisistaan erilleen). Jälkimmäinen voima pitää pallon kokoonpuristuneena – 20 N sisältää jousivoiman. Kontaktiaikana palloon kohdistuva keskimääräinen voima on siis 20 N riippumatta pallon kimmoisuudesta (COR-arvosta). Keskimääräinen voima ei riipu myöskään kontaktiajasta: t = 0,5 ms => ~ 20 N.
Tukivoimaa käyttäen tehtyä lyöntiä voidaan tarkastella superpositioperiaatteen mukaisesti analysoimalla erikseen lyöntiä ilman tukivoimaa lapaa kiihdyttämättä ja erikseen lavan kiihdyttämistä. Ne eroavat toistaan merkittävästi.
Lapaa kiihdyttämättä lyötäessä pallo saa lähtönopeuteensa tarvittavan liikemäärän kokonaisuudessaan siitä lavan liikemäärästä, joka lavalla on juuri ennen osumaa. Pallon liikemäärän lisääntyminen = lavan liikemäärän väheneminen => lavan nopeus hidastuu osuman aikana. Mitä enemmän lapa hidastuu, sitä suuremman lähtönopeuden pallo saa.
Kiihdytettäessä lapaa osuman aikana pallo ja lapa saavat liikemääränsä kiihdyttävästä voimasta. Kontaktiaikana lavan ja pallon keskikiihtyvyys a = F/(mb+mc) => vauhdin kasvu molemmilla sama: Δv = Ft/(mb+mc) eli Δv = at.
Mutta mutta … oikeastaan sanallisia selittelyjä ei tarvita. Viimeksi ja aiemminkin moneen kertaan esille ottamani kaava perustuu mekaniikan III lakiin. Jos sitä ei usko, niin ei usko voiman ja vastavoiman lakiakaan, ei fysiikan professoria, ei Tutelmania eikä muitakaan alan asiantuntijoita.
(Joku voisi ehkä kysyä, että eikö tuo kaava olisi pitänyt johtaa liikemäärän säilymisen perusteella. Vastaus on se, että liikemäärän säilymisen laki on suora seuraus voiman ja vastavoiman laista. Se ei kuitenkaan välttämättä sovellu käytettäväksi, jos mukana on ulkoisia voimia. Siksi lähdin liikkeelle voiman ja vastavoiman laista.)
Tarkennukseksi vielä: olen laskeskellut tässä ketjussa lähinnä vain sitä, kuinka suuren lisän osuma-aikainen kiihdyttäminen pallon lähtönopeudelle tuottaa. Tulos: ei juuri minkäänlaista. En kuitenkaan tarkoita sitä, että neuvo ’kiihdytä osuman läpi’ olisi hylättävä. On mahdollista, että tällä mielikuvalla/tekemisellä joku voi saada mailanpäälle suuremman nopeuden ja tarkempia lyöntejä, kuin ilman tuota mielikuvaa/tekemistä.
Jos uskoo löytäneensä itselleen sopivan svingitekniikan, niin siitä kannattaa pitää kiinni. Itseensä luottaminen on onnistuneiden lyöntien perusta.
Minunkin osaltani tämä taisi olla tällä erää tässä.
Juurikin niin👍 Eli jos lyöjä lyö 2 lyöntiä samalla lavannopeudella ja täydellisellä osumalla niin lyönnissä jossa on pienempi lavan hidastuvuus on enemmän tukivoimaa ja ”veto päällä”!
Siis sama mailanpään nopeus ja sama osumageometria. Toisessa lyönnissä ’tukivoiman’ aiheuttama osuma-aikainen lavan kiihtyvyys 0 ja toisessa a (ennen osumaa suurempi). Tässä tapauksessa todellakin näin käy. Edellisen viestini mukaisesti ’tukivoima’ lisää lavan nopeutta määrällä Δv = at. Esim. jos a on kohtuullinen 200 m/s^2 ja t = 0,5 ms, niin Δv = 0,1 m/s = 0,22 mph, eli tukivoimaa käytettäessä mailanpää hidastuu tuon verran vähemmän.
Yleisesti ottaen on kuitenkin niin, kuin edellisessä viestissäni kerroin (näin myös viimeisen lauseen osalta 😉)
Onkohan tässä pientä väärinkäsitystäkin käytetyistä termeistä johtuen? Kuten aikaisemminkin kirjoitin niin termi ”kiihdytys läpi osuman” on vain mielikuva jolla veto saadaan pysymään päällä läpi osuman joka taas tarkoittaa samaa kuin tuotettu tukivoima josta mielestäni Swingerkin kirjoittaa.
Itse osumassa en usko kiihdytystä tapahtuvan vaan hidastuksen vain olevan pienemmän kuin ns. vapaassa swingauksessa jossa voimantuotto lopetetaan aiemmin!
Tällaisessa ”tuetussa” suorituksessa taas lavan tehollinen massa on paljon suurempi kuin sen todellinen paino ja se taas saadaan aikaiseksi pitämällä osumassa grippi lavan etupuolella, jatkamalla vetoa, käyttämällä jäykempää vartta jne.
Näiden merkitykselle voi naureskella mutta suosittelen kokeilemaan 😉PG
Kantasi on siis ketjun aikana muuttunut. Hyvä!Mielestäni sanoin tämän jo aika pitkän aikaa sitten tämän, joten ei se pitkään aikaan ole muuttunut.
PG
Tarkennukseksi vielä: olen laskeskellut tässä ketjussa lähinnä vain sitä, kuinka suuren lisän osuma-aikainen kiihdyttäminen pallon lähtönopeudelle tuottaa. Tulos: ei juuri minkäänlaista.No tää oli hyvä tarkennus. Mietinkin että tämä ei oikein etene. Mutta, siis mulle ei tuota ainakaan tarvi enää todistella. Olin jo siirtyny aiheesta seuraavaan. Ehkäpä en osannut tuota sanoa riittävän selvästi.
PeWin
Onkohan tässä pientä väärinkäsitystäkin käytetyistä termeistä johtuen?Ilmeisesti on ollut. Ja, olen samaa mieltä että tukivoimalla on selvä merkitys, mutta tältä kierrokselta energiat on käytetty, vieterissä ei ole enää vetoa ja pallokin hukku outtiin.
2.4.2021 14:22:43 Swinger: Pallo saa siis (ko voiman vaikutuksen osalta) n. 6.5 kertaisen nopeuden kuin lapa (arvoilla lapa 300g ja pallo 46g), ja ne tapahtuu samassa ajassa joten kiihtyvyydetkin menee samassa suhteessa.
4.4.2021 12:02:19 Swinger: Lyhyesti, en usko Tutelmania. Uskon itseäni.
4.4.2021 20:18:12 Swinger: Kiihdytyksen vaikutus on marginaalinen, eli niin pieni ettei oleellisesti vaikuta.
5.4.2021 12:17:12 PG: Kantasi on siis ketjun aikana muuttunut. Hyvä!
6.4.2021 09:22:40 Swinger: Mielestäni sanoin tämän jo aika pitkän aikaa sitten tämän, joten ei se pitkään aikaan ole muuttunut.
Ymmärsin noista viesteistäsi, että kantasi muuttui 4.4.2021 klo 12 ja 20 välisenä aikana. Taisin ymmärtää väärin. Pahoittelut.
Swinger
PG: Tarkennukseksi vielä: olen laskeskellut tässä ketjussa lähinnä vain sitä, kuinka suuren lisän osuma-aikainen kiihdyttäminen pallon lähtönopeudelle tuottaa. Tulos: ei juuri minkäänlaista.
No tää oli hyvä tarkennus. Mietinkin että tämä ei oikein etene. Mutta, siis mulle ei tuota ainakaan tarvi enää todistella.
Tuo ei todellakaan ollut tarkoitettu sinulle Swinger, vaan PeWinille ja muillekin, jotka osallistuvat tähän ketjuun harvoin tai seuraavat sitä vain silloin tällöin.
Näiden kommentoimiesi asioiden lisäksi toin tuossa viestissäni esille pari uutta ja mielestäni hyvin oleellista näkökohtaa (vahvennettu). Oletko edelleen samaa mieltä, kuin viestissäsi 2.4.2021 14:22 ? Tuo mielipidehän pitää sisällään sen, että (laskelmiesi mukaan) tukivoima lisää pallon lähtönopeutta 1,8% ja lyönnin pituutta 5-6 m, jolloin tukivoimalla on merkitystä pallon lähtönopeuteen.
PG
Ymmärsin noista viesteistäsi, että kantasi muuttui 4.4.2021 klo 12 ja 20 välisenä aikana.Sanoin viestissä 14.1.2021 mm. seuraavaa:
mailanpään lisäkiihtyyvyden osuman keston aikana osalta tilanne on selvä (ei merkittävää vaikutusta),
joten on toi asia ollu mulle selvää jo pitkään.
Tästä taas en ole mieltäni muuttanu:
4.4.2021 12:02:19 Swinger: Lyhyesti, en usko Tutelmania. Uskon itseäni.
Tää puolestaan liittyy siihen että tuon osumanaikaisen voiman seurauksena Tutelmamin mukaan pallolle ja lavalle tulisi sama [lisä]nopeus. Tämä siis siitä Tutelman linkistä jonka viimeksi laitoit ja luin. Toi mun em laskutulos voi hyvin olla luvuiltaan väärin, mutta olen sitä mieltä että Tutelman oikaisee tuossa kohtaa jostain syystä, ja pallolle tulee isompi nopeus kun lavalle, johtuen pallon puristumisen ja vapautumisen jousivoimista. [Ja energiat ja liikemäärät pitää toki säilyä, en ole fysiikan lakeja tässä muuttamassa]
Huomasitko tätä:
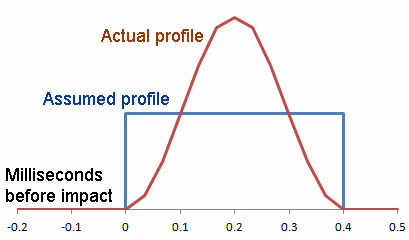
DEPENDENCE ON FORCE PROFILE DURING IMPACT
One last point: These calculations are based on a constant force — the average force — during contact between clubhead and ball. The blue force-vs-time profile in the picture shows this; during impact, the force is some constant value, and it is zero all other times. Obviously this is contrary to fact; the force starts small, increases as the ball compresses, and decreases as the ball releases and leaves the clubface. In other words, the red force-vs-time profile is what is really happening.So we need to show that it doesn’t matter; any force profile that gives the same average force will give the same final velocities. (”The same average force” means the same area under the profile curve.)
-
JulkaisijaArtikkelit
Etusivu › Foorumit › Kilpagolf & harjoittelu › Voimaa osumaan – uusi kierros


